Радиус окружности, вписанной в правильный шестиугольник, равен 2√ 3 см. Найти площадь и периметр шестиугольника.
Периметр многоугольника равен сумме его сторон.
Периметр правильного шестиугольника
Р=6а
Правильный шестиугольник состоит из 6 равных правильных треугольников.
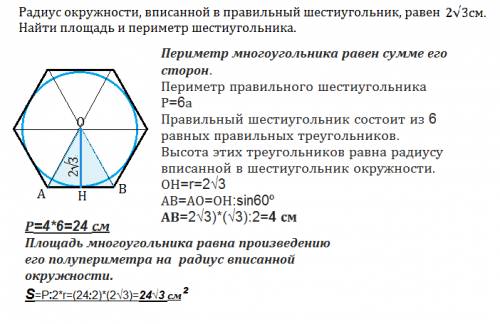
Высота этих треугольников равна радиусу вписанной в шестиугольник окружности. (см. рис.)
ОН=r=2√3
АВ=АО=ОН:sin60º
АВ=2√3)*(√3):2=4 см
Р=4*6=24 см
Площадь многоугольника равна произведению его полупериметра на радиус вписанной окружности.
S=P:2*r=(24:2)*(2√3)=24√3 см²
Задача решается через векторы.
Построим вектор
Середина D отрезка AB может быть найдена откладыванием половины вектора
Итак D( -9+4, 10-3 ) = D( -5, 7 ) ;
От точки D нужно отложить вектор высоты
Вектор высоты
(I)
Таким образом вектор
Вектор
Аналогично, AB = 10
При этом, поскольу треугольник равносторонний, то значит его высота составляет
Значит
В итоге
Откладываем этот вектор в разные стороны (+\-) от точки D( -5, 7 ) и получаем:
ОТВЕТ: