3 см
Чертеж в приложении.
Объяснение:
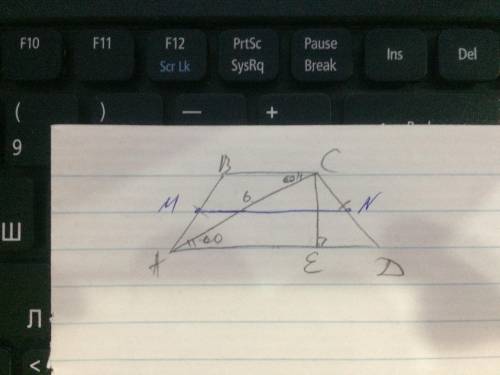
1. Опустим перпендикуляр СЕ в трапеции от меньшего основания к большему. Эта высота разделит большее основание на два отрезка. По свойству равнобедренной трапеции (ЕD - меньший равен половине разности оснований, AE - больший равен полусумме оснований) больший отрезок = средней линии, тк средняя линия тоже = полусумме оснований ;
2. рассм треуг АСЕ- прямоуг (тк СЕ перпенд АD):
тк сумма углов треуг =180, то уг АСЕ= 180-уг САЕ-уг АЕС=180-60-90=30 градусов;
тк АЕ- катет против 30 гр, то АЕ=1/2гипотенузы=1/2 *АС=1/2 * 6=3см
значит, средняя линия MN =3 см
Если что-то непонятно , пишите в комментах.
1 задача:
Доведения:
Рассмотрим ΔABD и ΔАВС
1) АВ = ВС (ΔАВС - равнобедренный с основанием АС)
2) AD = DC (ΔАВС - равнобедренный с основанием АС)
3) BD - общая.
Итак, ΔABD = ΔСВС за III признаком piвностi треугольников.
3 этого следует, что ∟ABD = ∟CBD. Тогда BD - биссектриса ∟АВС.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой, поэтому АЕ = ЕС.
2 задача
Рассмотрим ΔАВС - равнобедренный (АВ = ВС),
тогда ∟А = ∟C (свойство равнобедренного треугольника).
Рассмотрим ΔАВК и ΔСВМ.
1) АВ = ВС (по условию)
2) ∟А = ∟C (ΔАВС - равнобедренный)
3) ∟ABK = ∟CBM (по условию).
Итак, ΔАВК = ΔСВМ за II признаком piвностi треугольников.
3 этого следует pавность всех соответствующих Элементы, а именно ВМ = ВК.