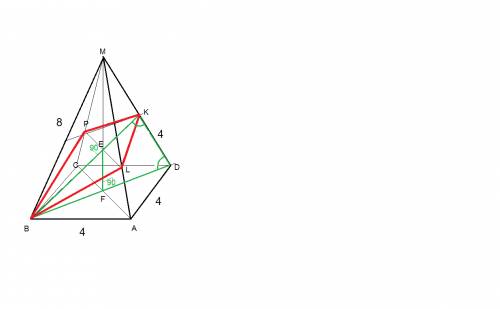
искомое сечение - симметричный четырехугольник BPKL
диагонали PL , BK пересекаются под углом 90 град
по условию
стороны основания AB=BC=CD=AD =4
боковые ребра MA=MB=MC=MD =8
точка К - середина ребра MD ; KD = MD /2 = 8/2=4
ABCD -квадрат
диагональ AC = BD = 4√2
пересечение диагоналей точка F : BF =FD = BD/2 =4√2 /2 =2√2
BK - медиана треугольника MBD
длина медианы BK = 1/2 √(2 BM^2 +2 BD^2 - MD^2 ) =1/2 √(2*8^2 +2*(4√2)^2 - 8^2 ) =4√2
по теореме косинусов
cos KBD = ( KD^2 - (BK^2+BD^2) )/ (-2*BK*BD)= ( 4^2 - ((4√2)^2+(4√2)^2) )/ (-2*4√2*4√2)= 3/4
MF - высота
треугольник EBF - прямоугольный
BE = BF / cos KBD = 2√2 / 3/4 = 8√2/3
KE = BK - BE =4√2 -8√2/3 =4√2/3
по теореме Пифагора EF =√(BE^2 - BF^2) =√( (8√2/3)^2 - (2√2)^2) =2√14/2
MF - высота
треугольник MFB - прямоугольный
по теореме Пифагора MF =√( MB^2 -BF^2) =√( 8^2- (2√2)^2 ) =2√14
ME =MF -EF =2√14 -2√14/2 = 2√14/2
треугольники MPL ~ MCA подобные
PL / AC = ME /MF ; PL = AC * ME /MF = 4√2 * 2√14/2 /2√14 =2√2
площадь сечения(четырехугольника BPKL)
Sс = PL*BK *sin<BEP /2 = 2√2*4√2*sin90 /2 = 8
ответ 8
В условии не хватает слов "параллельно АС". В противном случае задача не имеет решения (точнее одного решения, сами по себе решения есть, но - не интересные :) одно из них - треугольник MBD).
Пусть b=8; a = 4; О - центр основания, МО - высота пирамиды, сечение пересекает MD в точке Q (MQ = QD), МС в точке Р, MA - в точке G, МО в точке К. Надо найти площадь четырехугольника BGQP.
Плоскость сечения II АС, поэтому GP II AC, откуда MG/GA = МК/КО = MP/PC = 2/1; поскольку BQ и MO - медианы, и К - точка пересечения медиан треугольника MBD.
то есть
GP = (2/3)*AC = a*2√2/3; (из подобия треугольников AMC и GMP)
И еще, поскольку у квадрата диагонали перпендикулярны, AC перпендикулярно плоскости треугольника MDB, откуда следует, что GP перпендикулярно BQ, то есть площадь S четырехугольника BGQP равна S = BQ*GP/2;
Остается найти медиану m = BQ равнобедренно треугольника MDB с боковыми сторонами MD = MB = b = 8; и основанием BD = a√2; (a = 4);
(2*m)^2 = 2(a√2)^2 + b^2;
m = (1/2)*√(4*a^2 + b^2);
S = (1/2)*(a*2√2/3)*(1/2)*√(4*a^2 + b^2) = (1/6)*a*√(8*a^2 + 2*b^2);
ну и надо подставить числа.
если b = 2*a, то S = (2/3)*a^2 = 32/3;
27.04.2015
Мне предложили тут что-то изменить. Якобы ответ должен быть в 2 раза меньше. Я очень буду рад, если мне предложат грамотный анализ решения. Но я могу показать на пальцах, что ответ верный. Это как раз очень просто. В сечении получается дельтоид, у которого одна из диагоналей BQ = BD; а вторая - GP = (2/3)*AC; отсюда мгновенно понятно, что площадь сечения составляет 2/3 площади основания.
(площадь сечения) = BQ*GP/2 = (2/3)*BD*AC/2 = (2/3)*(площади основания) = (2/3)*4^2 = = 2*16/3 = 32/3;
любые попытки найти тут ошибку могут вызвать только улыбку :