Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
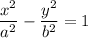, где а - действительная полуось, b - мнимая полуось
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
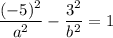
Также распишем эксцентриситет гиперболы:
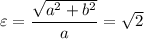
Преобразуем. Возведем в квадрат:
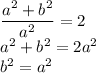
Подставим в уравнение с координатами выявленное соотношение:
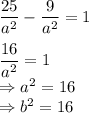
Все необходимые данные для записи уравнения есть:
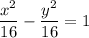
Поскольку квадрат мнимой полуоси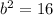 
, то ее длина - соответственно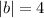 
Номер 1
Можно даже не вычислять,чему равны углы 1;2;3;
Два угла 30 градусов называются соответственными,если при пересечении двух прямых секущей соответственные углы равны,то прямые параллельны
<1=<30=30 градусов,как накрест лежащие,вообще-то-смотрятс каким из двух углом сравнивать
<1+<2=180 градусов,как односторонние
<2=180-30=150 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<3=<2=150 градусов,как вертикальные
Номер 2
<20=<2=<20 градусов,как вертикальные
Если угол 3 в 8 раз больше угла 2,то
<3=20•8=160 градусов
<3=20+160=180 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<4=<3=160 градусов,как накрест лежащие
<5=<2=20 градусов
Объяснение: