Тест по теме «Окружность»
1. Сколько существует различных случаев взаимного расположения прямой и окружности?
а) один; б) два; в) три.
2. Сколько существует различных случаев взаимного расположения двух окружностей?
а) один; б) два; в) три.
3. Две окружности касаются внешним образом. Радиус одной из них равен 2 см, а другой – 7 см. Найдите расстояние между центрами окружностей.
4. Как расположены прямая и окружность, если радиус окружности равен 9 см, а расстояние от её центра до прямой равно 5 см?
а) прямая и окружность имеют две общие точки;
б) прямая и окружность не имеют общих точек;
в) прямая и окружность имеют одну общую точку.
5. Радиусы двух окружностей равны 5 см и 8 см, а расстояние между центрами окружностей 13 см. Как расположены окружности относительно друг друга?
а) окружности не пересекаются;
б) окружности пересекаются;
в) окружности касаются друг друга.
6. При каком условии окружность и прямая не пересекаются (r – радиус окружности, d – расстояние от центра окружности до прямой)?
а) rd б) r в) r
7.Две окружности касаются внутренним образом. Радиус одной из них равен 5 см, а другой – 3 см. Найдите расстояние между центрами окружностей.
8. Как расположены прямая и окружность, если радиус окружности 6 см, а расстояние от её центра до прямой 7 см?
а) пряма и окружность имеют одну общую точку
б) прямая и окружность не имеют общих точек
в) прямая и окружность имеют две общие точки
9. Радиусы двух окружностей 3 см и 10 см, а расстояние между их центрами 17 см. Как расположены окружности относительно друг друга?
а) окружности не пересекаются
б) окружности пересекаются
в) окружности касаются друг друга
10. На рисунках изображены различные варианты расположения двух окружностей. Определите, на каком из рисунков изображены концентрические окружности.
1.
V = 96π см³
Sбок = 60π см²
2.
V = 54√2π см³
Sбок = 36π см²
Объяснение:
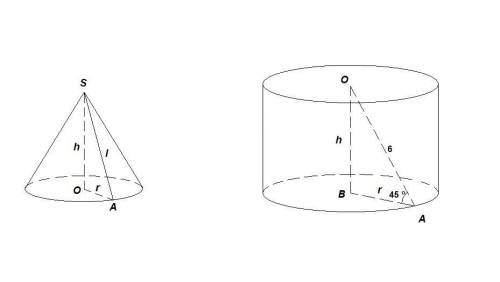
1.
r = 6 см, h = 8 см.
Из прямоугольного треугольника SOA по теореме Пифагора найдем образующую:
l = √(r² + h²) = √(36 + 64) = √100 = 10 см
V = 1/3 πr²h, где
r - радиус основания,
h - высота.
V = 1/3 π · 6² · 8 = 1/3 π · 36 · 8 = 96π см³
Sбок = πrl, где
r - радиус основания,
l - образующая.
Sбок = π · 6 · 10 = 60π см²
2.
ОА = 6 см
ΔОАВ прямоугольный равнобедренный (∠ОАВ = 45°), значит
r = h
По теореме Пифагора:
r² + h² = OA²
2r² = 36
r² = 18
r = 3√2 см
h = r = 3√2 см
V = πr²h
V = π · 18 · 3√2 = 54√2π см³
Sбок = 2πrh
Sбок = 2 · π · 3√2 · 3√2 = 36π см²