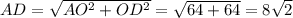
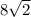
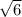 и ВС=
и ВС=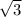 . АС - гипотенуза, АС=3. Чтобы узнать проекции катетов на гипотенузу, надо из вершины прямого угла опустить перпендикуляр на гипотенузу. Пусть это будет ВМ. Тогда АМ - проекция АВ, МС - проекция ВС. Пусть АМ=х, тогда МС=3-х, потому что АС=3. Тогда по формуле среднего геометрического ВМ=
. АС - гипотенуза, АС=3. Чтобы узнать проекции катетов на гипотенузу, надо из вершины прямого угла опустить перпендикуляр на гипотенузу. Пусть это будет ВМ. Тогда АМ - проекция АВ, МС - проекция ВС. Пусть АМ=х, тогда МС=3-х, потому что АС=3. Тогда по формуле среднего геометрического ВМ=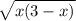 . А теперь рассмотрим прямоугольный треугольник АВМ. Запишем теорему Пифагора:
. А теперь рассмотрим прямоугольный треугольник АВМ. Запишем теорему Пифагора: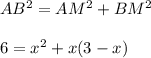
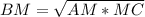
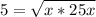
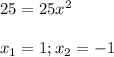
AM - перпендикуляр, МВ наклонная, АВ - проекция наклонной МВ на плоскость ΔАВС
МС - наклонная, АС - проекция наклонной МС
по условию АВ=ВС=АС=4 см. наклонные равны, => равны наклонные.
ΔВМС - равнобедренный. расстояние от точки М до прямой ВС - длина перпендикуляра МК -высоты равнобедренного треугольника ВМС.
или МК - наклонная, АК -проекция наклонной МК
Мк -высота правильного ΔАВС, вычисляется по формуле: h=a√3/2
h=4√3/2, АK=2√3 см
прямоугольный ΔМАК: по теореме Пифагора МК²=АК²+АМ²
МК²=(2√3)²+2². МК²=12+4, МК=4 см
ответ: расстояние от точки М до прямой ВС 4 см