Задача 1 ¹/₂П а²
не указана сторона шестиугольника
Объяснение:
Пусть R - радиус окружности, описанной около правильного шестиугольника, r - радиус окружности, вписанный в правильный шестиугольник.
Тогда площади кругов с этими радиусами:
Sо = 2ПR², Sв = 2Пr²
Площадь кольца:
S= Sо - Sв = 2ПR²- 2Пr² = 2П(R²-r²)
R = a, r=a×√3/2,
где а - сторона шестиугольника
S= 2П(R²-r²) = 2П×(а² - (√3/2а)²) = 2П×( а² - ³/₄а²) = 2П ×¹/₄а² = ¹/₂П а²
Задача 2
Объяснение:
Предисловие: Построим чертеж, докажем, что треугольники подобны, найдем коэффициент подобия
Решение.
Рассмотрим АОД и ВОС. Т.к. АВСД - трапеция, то ВС ║ АД.
∠СВД = ∠ВДА как накрест лежание (ВС ║ АД, ВД - секущая)
∠ВОС = ∠АОД как вертикальные
АОД и ВОС подобны по 2 углам.
Стороны ВС и АД - соответственные
Коэффициент подобия : k= ВС/АД = 4/16 = 1/4
SАОД / SВОС = k² = 1/16
Для вычисления площадей надо знать высоту.
Уточните условие задачи
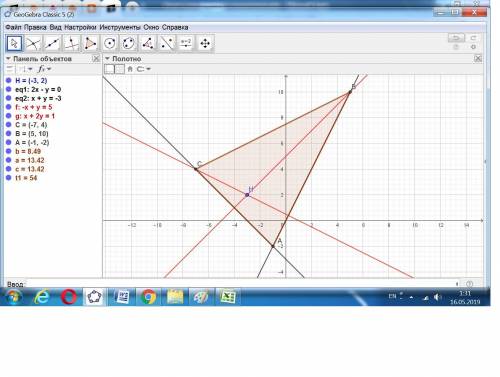
Даны уравнения двух сторон треугольника. Пусть это будут:
АВ: 2x-y = 0, АС: x + y + 3 = 0.
Запишем их в виде уравнений с угловым коэффициентом.
АВ: у = 2x, АС: у = -x - 3 = 0.
Одну вершину треугольника находим как точку пересечения прямых, содержащих 2 стороны треугольника.
Точка А. 2x - y = 0
x + y + 3 = 0 сложение
3х + 3 = 0 х = -3/3 = -1, у = 2х = 2*(-1) = -2.
Далее находим уравнения высот, проходящих через точку Н (-3; 2) с учётом, что их угловой коэффициент обратен угловому коэффициенту стороны, к которой они проведены.
к(ВН) = -1/к(АС), ВН: 2 = 1*(-3) + в, отсюда в = 2 + 3 = 5.
Уравнение высоты ВН: у = х + 5.
Аналогично определяем СН: 2 = (-1/2)*(-3) + в, в = 2 - 3/2 = 1/2.
Уравнение высоты СН: у = (-1/2)х + (1/2).
Далее определяем координаты вершин В и С как точек пересечения соответственно прямой АВ и высоты ВН, прямой АС и высоты СН.
Точка В: (5; 10), точка С: (-7; 4).
Теперь можно получить ответ.
Уравнение стороны ВС определяем как прямую , проходящую через 2 точки.
ВС: (х - 5)/(-7 - 5) = (у - 10)/(4 - 10),
(х - 5)/(-12) = (у - 10)/(-6) это каноническое уравнение прямой ВС.
Сократив знаменатели на -6, получаем х - 5 = 2у - 20.
Уравнение ВС в общем виде х - 2у + 15 = 0.
Оно же в виде уравнения с угловым коэффициентом:
ВС: у = (1/2)х + (15/2).
ответ: S= 1/2 ah= 1/2 • 6 • 1 = 3 см2
Объяснение: