Дано :
параллелограмм NPKA
<ANK = 45°
<KNP = 65°
Найти:
<А, <К, <Р, <N, <NKA, <NKP = ?
<N = <ANK + <KNP = 45° + 65° = 110°
<N = <K = 110° (св-во параллелограмма - противоположные углы равны)
<А = 180° - <К = 180° - 110° = 70° (свойство параллелограмма - углы, прилежащие к любой стороне, в сумме равны 180°)
<Р = <А = 70° (св-во параллелограмма - противоположные углы равны)
<NKA = <KNP = 65° (н.л. при NP//AK и секущей NK)
<NKP = <K - <NKA = 110° - 65° = 45°
ответ: <А = <Р = 70° ; <К = <N = 110° ; <NKA = 65° ; <NKP = 45°
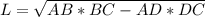 .
.
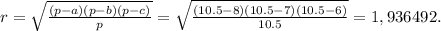
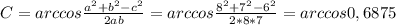 .
.
Один из углов в прямоугольном треугольнике 30, тогда меньший катет половина гипотенузы. Тогда пусть меньший катет х.Тогда х+2х=3х=75, поэтому х(меньший катет)=25, 2х(гипотенуза)=50. По теореме пифагора 2 катет равен корню из суммы квадрата катета и квадрата гипотенузы или если говорить математическим языком: 2 катет=√(x²+(2x)²)=√(x²+4x²)=√5x²=25√5cm