75 см²
Объяснение:
Прямоугольные треуг-ки ВНС и АН1С подобны по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого. В нашем случае углы АН1С и ВНС прямые, а угол С - общий. Для подобных треугольников можно записать отношение сходственных сторон:
ВН:АН1=10:12, k=5/6, СН:СН1=5:6, отсюда
CH1=6CH:5
В прямоугольном треуг-ке АН1С по теореме Пифагора находим АС:
АС²=AH1²+CH1²
Т.к. в равнобедренном треуг-ке АВС высота ВН, проведенная к основанию, является также и медианой, то СН=1/2АС, и выражение CH1=6CH:5 примет такой вид:
СН1=3АС:5.
Это значение для СH1 будем использовать в вычислении по теореме Пифагора:
АС²=12² + 9AC²/25
AC² - 9AC²/25=144
16AC²=3600
AC² = 225
AC=15 см
S ABC = 1/2AC*BH=7,5*10=75 см²
ответ: 21 см
( Среднюю линию нарисуйте сами на трапеции )
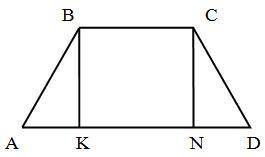
Дано :ABCD- трапеция, АВ=СD=6 см, ∠А=60° ,АD=24 см
Найти : среднюю линию трапеции.
Решение: Средняя линия трапеции - отрезок соединяющий середины боковых сторон(АВиСD) и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
Необходимо найти ВС, для этого из вершин В и С проведём высоты к основанию АD ( ВК ⊥АD и СN⊥АD ),
Рассмотрим ΔАВК, где АВ=6см, ∠А=60°, ∠К=90°, по теореме о сумме трёх углов треугольника ∠АВК= 180°-(90°+60°)=30°.
катет АК лежит против угла 30° прямоугольного треугольника АВК и равен половине гипотенузи АВ:
АК=60см:2=3 см.
Соответственно рассмотрев ΔСND , где ∠N=90°, ∠D=60°( как угол при основании равнобедренной трапеции) ∠DСN= 180°-(90°+60°)=30°.
ND =6см:2=3см( как катет , лежащий против угла 30° прямоугольного треугольника СND).
так как ВС║АD( как основания трапеции) ,ВК║СN( как перпендикуляры одной прямой) и ∠К=∠N=90°, то КВСN- прямоугольник , где ВС= КN
КN= АD-АК-ND=24-3-3=18(см), ВС= 18 см
Найдём длину средней линии: L=(АD+ВС):2=(24+18):2=21(см)
60; 60; 60
Объяснение:
Рассмотрим прямоугольный треугольник: боковая сторона, высота, половина основания. Боковая больше высоты в √3/2 раз, значит высота лежит против угла в 60°, а это угол при основании равнобедренного треугольника, значит все углы равны