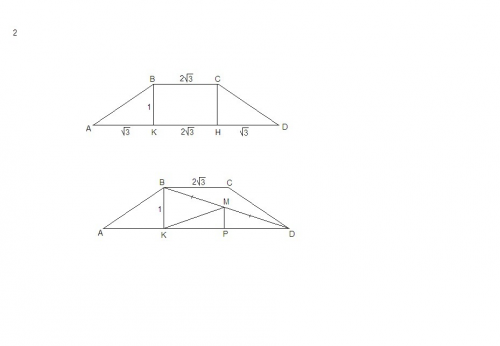
Рисуем обычную треугольню пирамиду. В основании тр-к АВС и вершина Д. На середине ВД отмечаем т.М.Соединяем А и М, С и М. На середине АС ставим т. К , соединим т К и т М. Чертеж готов.В правильном тетраэдре все ребра равны, обозначим ребро "а", все грани равны.Значит, чтобы найти полную поверхность тетраэдра надо найти площадь одного тр-ка и умножить на 4. АМ и СМ- высоты равност-х тр-ков, АМ=СМ=аV3/ 2, (V-обозначение корня), МК-высота равноб-го тр-ка АМС(и медиана), из тр-ка АМК АК=а/2 КМ^2=AM^2-AK^2=3a^2/4-a^2/4=2a^2 /4, KM=aV2 /2, S(AMC)=1/2*a*aV2 /2, 9=a^2 /4, a^2=36, a=6/
S(ABC)=1/2*6*6*sin60=18*V3 /2=9V3, тогда S(полной пов-ти)=4*9V3=36V3
CO = 4
OB = 12
Объяснение:
Углы пересечения прямой с параллельными прямыми одинаковые.
Т.е. ∠A = ∠B, а ∠С = ∠D
Поскольку сумма углов треугольника = 180°, значит и 3-ий угол треугольников AOC и BOD совпадает. Следовательно эти треугольники подобные. Стороны подобных треугольников пропорциональны.
BD/AC = 10/2 = 2. Т.е. коэффициент подобия = 2
CO = OD/2 = 4
OB = AO*2 = 12