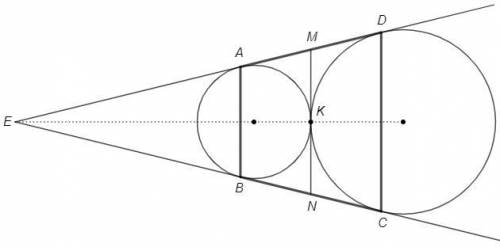
Пусть AD и BC пересекаются в точке E.
Отрезки касательных из одной точки равны, EA=EB, ED=EC.
△AEB, △DEC - равнобедренные => EAB =90 -E/2 =EDC => AB||DC
ABCD - трапеция
MA=MK=MD, NB=NK=NC (отрезки касательных из одной точки)
MN - средняя линия трапеции ABCD
MN =(AB+CD)/2 =(8+13)/2 =10,5
NB=NK=NC => NK=BC/2
Центры лежат на биссектрисе угла E (т.к. окружности вписаны в угол).
Точка внешнего касания окружностей K лежит на линии центров, то есть на биссектрисе угла E.
MN||AB => △MEN~△AEB =>
△MEN - равнобедренный, EK - биссектриса и медиана, NK=MN/2
BC =MN =10,5
Найдем сторону этого квадтара (ребро при основании)
АВ = √18 = 3√2 см
ВД1 - диагональ призмы.
Найдем ВД - диагональ основания
ВД = 3√2 * √2 = 6 см
Так как диагональ ВД1 наклонена к плоскости основания по углом 45, то треуг. ВВ1Д1 прямоугольный и равнобедренный. Высота призмы ВВ1 = ВД = 6 см.
Площадь боковой поверхности цилиндра, описаного около призмы равна произведению длины окружности в основании на высоту цилиндра.
Высота цилиндра равна высоте призмы, т.е. 6 см.
Диаметром окружности является диагональ основания призмы ВД.
S (боковое) = П * 6 * 6 = 36*П см.