Пирамида пересечена плоскостью, параллельной основанию. Площадь основания равна 2400 дм2, а площадь сечения равна 6 дм2. В каком отношении, считая от вершины, плоскость сечения делит высоту пирамиды?
(Вводи сокращённое отношение!)
Сечение, которое проведено параллельно основанию шестиугольной пирамиды, делит высоту пирамиды в отношении 5 : 8, считая от вершины. Вычисли площадь сечения, если площадь основания равна 676 дм2
Пирамида пересечена плоскостью, параллельной основанию,
которая делит высоту пирамиды в отношении 3 : 7, считая от вершины.
Вычисли площадь основания, если площадь сечения равна 27 дм2.
Sосн. =
дм2.
Впиши пропущенное слово:
если пирамида пересечена плоскостью, которая параллельна основанию, то площади сечения и основания относятся как
расстояний от них до вершины пирамиды.
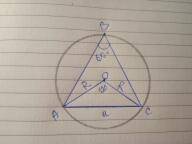
Объяснение:
1)Рассмотрим △АВС.
Так как углы при основании АС равны (∠А =∠С), то △АВС - равнобедренный.
В равнобедренном треугольнике боковые стороны равны.
АВ=ВС.
2) Рассмотрим △BDC и △FDE.
BD=DF, CD= ED, ∠EDF =∠CDB - как вертикальные.
Следовательно △BDC = △FDE по двум сторонам и углу между ними ( первый признак равенства треугольников).
Из равенства треугольников следует равенство сторон: BC = EF.
Значит АВ=ВС=EF.
3) Рассмотрим △EHF и △KHF.
EH = KH, ∠EHF =∠KHF, HF - общая.
△EHF = △KHF по двум сторонам и углу между ними ( первый признак равенства треугольников).
Из равенства треугольников следует равенство сторон: EF = FK.
Значит АВ=ВС=EF = FK
Таким образом мы доказали, что АВ = FK
Для доказательства равенства двух отрезков использовали следующие :
Рассматривали эти отрезки как стороны двух треугольников, и доказывали, что эти треугольники равны. Рассматривали эти отрезки как стороны одного треугольника, и доказывали, что этот треугольник равнобедренный.