Задания по теме «Пирамида»
1. Сторона основания правильной треугольной пирамиды равна 9,
боковое ребро равно 6. Найдите угол между боковым ребром
пирамиды и плоскостью ее основания. ответ дайте в градусах.
2. Апофема правильной треугольной пирамиды равна 2√7, боковое ребро
равно 7. Найдите угол между плоскостью боковой грани пирамиды и
плоскостью ее основания. ответ дайте в градусах.
3. Основанием пирамиды SАBC является прямоугольный треугольник
АВС, у которого гипотенуза АС равна 20, катет АВ равен 16. Боковое
ребро SC перпендикулярно плоскости основания и равно 5. Найдите
длину ребра SB.
4. Основанием четырехугольной пирамиды PABCD является ромб ABCD,
в котором АС = 6, ВD = 8. Боковое ребро РА перпендикулярно к
плоскости основания пирамиды и равно 4. Найдите расстояние до
плоскости BPD от точки :
а) А;
б) Е – середины ребра ВС.
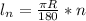 , где n - градусная мера соответственного центрального угла.
, где n - градусная мера соответственного центрального угла.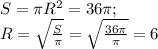 , где S - площадь круга.
, где S - площадь круга.
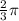 см.
см.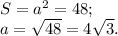
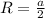 , где a - сторона квадрата.
, где a - сторона квадрата.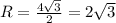
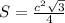 , где c - сторона правильного треугольника.
, где c - сторона правильного треугольника.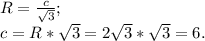
 .
.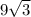 см.
см.
Опустим перпендикуляр AE из вершины A на прямую CB. Площадь трапеции AECD равна сумме площадей параллелограмма ABCD и треугольника AEB. Опустим перпендикуляр DF из вершины D на прямую CD. Тогда площадь трапеции AECD равна сумме площадей прямоугольника AEFD и треугольника DFC. Прямоугольные треугольники AEB и DFC равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника AEFD, т.е. равна AE • AD. Отрезок AE – высота параллелограмма, соответствующая стороне AD, и, следовательно, S = a • h. Теорема доказана.