Question

Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. найдите отношение объёмов шара и цилиндра. решить, мне нужно подробное решение, от этой контрольной зависит оценка в атестате

Answer 1

в сечении квадрат, а-сторона куба, значит радиус основания а/2

Vц=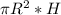$\pi R^2*H$ H в нашем случае равен a

Vц=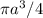$\pi a^3/4$

радиус шара равен половине высоте цилиндра,т.е. H/2 или а/2

Vш=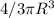$4/3 \pi R^3$

Vш=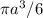$\pi a^3/6$

Vш/Vц=$(\pi a^3/6)/(\pi a^3/4)=2/3$