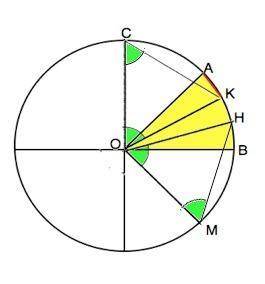
Дан угол АОВ=45°.
Из О как из центра чертим окружность произвольного радиуса. Проводим через О общепринятым перпендикулярно стороне ОВ прямую до пересечения с окружностью – диаметр.
Угол АОС=АОВ=45°.
Тем же радиусом из т. С делаем насечку в т. К на дуге АВ, т. К соединяем с т.О
Угол СОК=60° ( треугольник АОК - равносторонний)
Угол АОК=∠СОК-∠СОА=60°-45°=15°
а) Проводим биссектрису ОН угла КОВ. Данный угол поделен на 3 равные части. Или:
б) раствором циркуля, равным хорде АК. от т. В отмечаем на дуге АВ точку Н и соединим ее с О.
АОК=КОН=НОВ=15°.
-----------
Как вариант можно отложить от ОВ угол ВОМ=45° и от т.М тем радиусом ОВ отметить на дуге АВ т.Н.
1.
Внешний угол при вершине В равне сумме двух внутренних углов, не смежных с углом В.
Следовательно, сумма двух внутренних равна 40 градусов. Так как один из острых углов равен 20 градусов, второй угол тоже 20 градусов. Треугольник АВС - равнобедренный.
Сторона АВ равна стороне ВС
2.
Если два угла в треугольнике равны, третий угол тоже равен. Гипотенузы в этих треугольниках равны. Поэтому и треугольники равны.
3.
Наверное, нужно доказать, что угол А = углу DВC?
Треугольника АВС и АDВ подовбны .У них общий угол А и второй - прямой. Следовательно, Уол АВD= углу С. Подобен им и треугольник ВDС по той же причине, только здесь с большим треугольником у треугольника ВDС общим углом является угол С. По этой причине угол А = углу DВС.
Если угол А меньше угла С, то AD>DC, потому что против большего угла лежит большая сторона.