64-2пR
скореее всего так,хотя насчет минуса я не уверегна
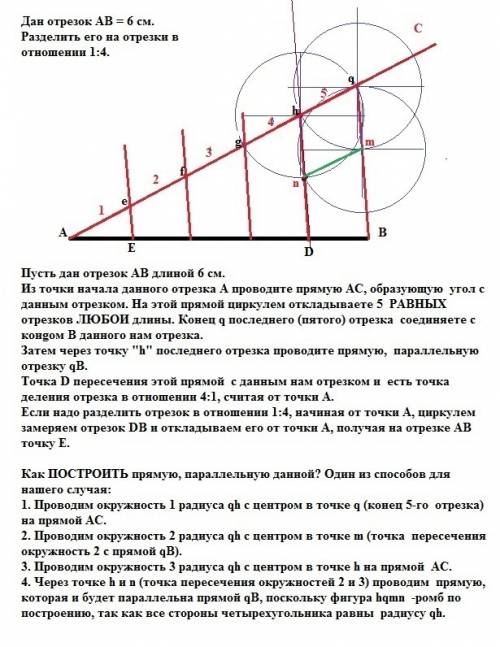
Задача на построение циркулем и линейкой обычно подразумевает наличие циркуля и линейки без делений. Пусть ДАН отрезок АВ длиной 6 см.
Из точки начала данного отрезка А проводим прямую АС, образующую угол с данным отрезком. На этой прямой циркулем откладываем 5 РАВНЫХ отрезков ЛЮБОИ длины. Конец q последнего (пятого) отрезка соединяем с конgом B данного нам отрезка.
Затем через точку "h" последнего отрезка проводим прямую, параллельную отрезку qВ.
Точка D пересечения этой прямой с данным нам отрезком АВ и есть точка деления отрезка в отношении 1:4, считая от точки В.
Если надо разделить отрезок в отношении 1:4, начиная от точки А, циркулем замеряем отрезок DB и откладываем его от точки А, получая на отрезке АВ точку Е.
Как ПОСТРОИТЬ прямую, параллельную данной? Один из для нашего случая:
1. Проводим окружность 1 радиуса qh с центром в точке q (конец 5-го отрезка) на прямой АС.
2. Проводим окружность 2 радиуса qh с центром в точке m (точка пересечения окружность 2 с прямой qВ).
3. Проводим окружность 3 радиуса qh с центром в точке h на прямой АС.
4. Через точке h и n (точка пересечения окружностей 2 и 3) проводим прямую, которая и будет параллельна прямой qB, поскольку фигура hqmn - ромб по построению, так как все стороны четырехугольника равны радиусу qh.
если опустить высоты из концов вехнего основания на нижнее и обозначить отсекаемые куски нижного отснования (от конца основания до ближайшего основания высоты) за x и y, то есть 2 уравнения.
x+y = 18-10 = 8;
17^2 - y^2 = 15^2 - x^2;
Я намеренно не буду решать это очень простую систему, а просто замечу, что 8, 15 и 17 - пифагоровы числа, то есть фигура с такими сторонами - прямоугольный треугольник. Поэтому x = 0 (ну решите системку сами, увидите:)). Итак, высота равна 15 :)));
Осталось понять, что проведенная через точку пересячения диагоналей высота делится точкой пересечения в отношении 18/10, то есть 9/5 (как основания, следует из подобия треугольников, образованных диагоналями и основаниями), поэтому длинна искомого отрезка равна
15*9/(9+5) = ну очень сложный ответ 135/14
второй 15*5/14 =75/14
Странно, кривой какой-то ответ, хотя 135+75=210, как и должно быть
за Бенедикта Камбербэтча :)))
У вписанной в квадрат окружности диаметр равен стороне. Поэтому длинна окружности равна числу пи, умноженному на сторону. То есть 8*pi.
То, что центр вписанной окружности равноудален от всех 4 сторон, означает, что он совпадает с центром квадрата (просто центр квадрата, он же - точка пересечения диагоналей, равноудален от всех сторон, а двух таких точек не может быть (потому что не может быть никогда:), на самом деле легко показать, что любая другая точка в квадрате НЕ равноудалена от сторон, всё это выходит за рамки задачи - это просто немного теории). Далее, прямая, соединяющая точки касания, является диаметром (перпендикуляр к касательной всегда пройдет через центр окружности) и равна по длине стороне, поскольку это просто перпендикуляр к стороне через её середину. Напомню, что все стороны квадрата равны между собой :))) По-моему, объяснений довольно. :)