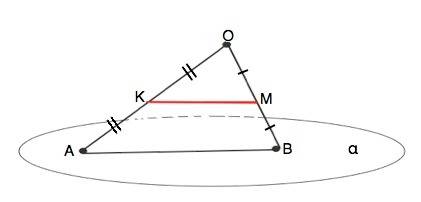
т.А и т.В лежат в плоскости альфа.
Если две точки прямой принадлежат плоскости, то все точки этой прямой принадлежат данной плоскости. ⇒
Прямая АВ лежит в плоскости альфа.
Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну (аксиома).⇒
Точки А, О, В лежат в одной плоскости.
К и М - середины боковых сторон ∆ АОМ. ⇒
КМ - средняя линия ∆ АОМ. ⇒ КМ║АВ (свойство)
КМ не лежит в плоскости альфа и параллельна АВ, лежащей в плоскости альфа.
Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, принадлежащей этой плоскости, то она параллельна плоскости.⇒
КМ параллельна плоскости альфа
Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Осноположником геометрии можно считать Евклида. В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». В развитии Геометрия можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.
Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Геометрия, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.Геоме́трия (от др. ... γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.
Дано:
В ABCD:
∠ABD=∠BDA=90°
AD=BC
Доказать: AB=DC
Доказательство.
По условию ∠ABD=∠BDA=90°, поэтому ΔBDA и ΔBDC прямоугольные.
Тогда верна теорема Пифагора для обоих треугольников. Имеем:
а) для ΔBDA: AD²=AB²+BD² или BD²=AD²-AB²
б) для ΔBDC: BC²=CD²+BD² или BD²=BC²-CD².
Отсюда
AD²-AB² = BC²-CD²
или из-за AD=BC:
BC²-AB² = BC²-CD² или AB² = CD².
Последнее означает AB = CD, что требовалось.
Подробнее - на -