Радиус OK окружности проведен из центра O и перпендикулярен хорде ML. ОК пересекается с хордой ML в точке N. Найдите длину хорды ML, если известно, что OK=10 см, NK=2

👇

Открыть все ответы

Ответ:

Hdzf2002

09.07.2020

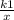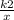Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y = $\frac{k1}{x}$ и y = $\frac{k2}{x}$ (k1, k2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что k1 * k2 = 144. Найдите наименьшую возможную длину отрезка OM.В ответ запишите квадрат длины ОМ.

Объяснение:

Прямая АВ , проходящая через начало координат имеет вид у=кх

Найдем точки пересечения этой прямой и гипербол:

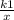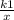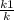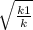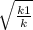y = $\frac{k1}{x}$ и у=кх → $\frac{k1}{x}$ = кх , х²= $\frac{k1}{k}$ ; x = $\sqrt{\frac{k1}{k} }$ ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* $\sqrt{\frac{k1}{k} }$ .

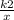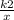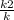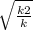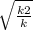y = $\frac{k2}{x}$ и у=кх → $\frac{k2}{x}$ = кх , х²= $\frac{k2}{k}$ ; x = $\sqrt{\frac{k2}{k} }$ ( т.к. точка пересечения в 1 четверти , то х>0 ). Тогда у= к* $\sqrt{\frac{k2}{k} }$ .

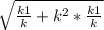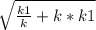По свойство касательной и секущей проведенных из одной точки ОМ²=ОА*ОВ. Найдем ОА и ОВ по формулам расстояния между точками : ОА= $\sqrt{\frac{k1}{k} +k^{2}*\frac{k1}{k} }$ = $\sqrt{\frac{k1}{k} +k*k1}$ ,

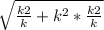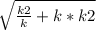ОB= $\sqrt{\frac{k2}{k} +k^{2}*\frac{k2}{k} }$ = $\sqrt{\frac{k2}{k} +k*k2}$ .

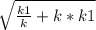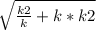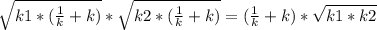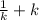Тогда ОМ²= $\sqrt{\frac{k1}{k} +k*k1}$ * $\sqrt{\frac{k2}{k} +k*k2}$ = $\sqrt{k1*(\frac{1}{k}+k) } *\sqrt{k2*(\frac{1}{k}+k) } =( \frac{1}{k}+k) *\sqrt{k1*k2}$ . Т.к $\frac{1}{k}+k$ ≥2 ,по следствию из неравенства о среднем арифметическом и среднем геометрическом , то принимает наименьшее значение равное 2 , а к1*к2=144, то ОМ²=2*√144=2*12=24.

===========================================

Свойство касательной и секущей проведенных из одной точки : "Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью."

Формула расстояния между точками d=√( (х₁-х₂)²+(у₁-у₂)² ), где (х₁;у₁ ), (х₂;у₂ ) -координаты концов отрезка.