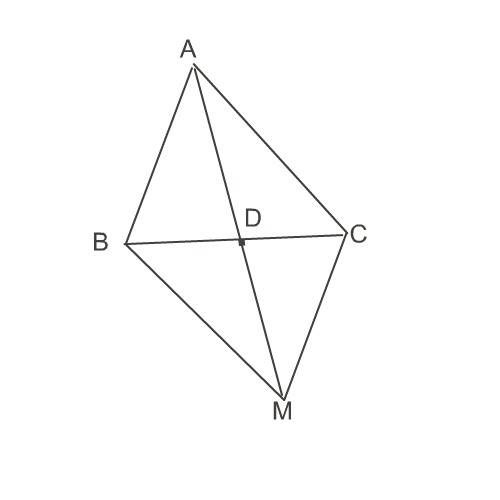
Делаем рисунок.
Продлим медиану АD на ее длину д и соединим конец М этого отрезка с вершинами В и С треугольника.
Получился параллелограмм,
в котором медиана - его длинная диагональ и делит параллелограмм на два равных треугольника:
Δ АСМ =Δ АВМ
Стороны этих треугольников равны 27см, 29 см и 26*2=52 см
По формуле Герона найдем площадь такого треугольника.
........_____________
S =√p(p-a)(p-b)(p-c)
p-полупериметр треугольника АСМ
р=(52+27+29):2= 54
........________________________
S =√54(54-52)(54-29)(54-27)
Не буду приводить вычисления, они стандартны, Вы сделаете их без труда.
S Δ АВМ=270 см²
А так как Δ АВМ - половина параллелограмма АВМС, то он равновелик треугольнику АВС, который тоже является половиной этого параллелограмма.
Площадь треугольника АВС =270 см²
Сделаем рисунок.
Соединим точку Е с вершиной С.
Найдем величину угла А
∠А=180°-23°-41°=116°
Так как АЕ=АС, получившийся Δ ЕАС - равнобедренный.
Поскольку в равнобедренном треугольнике биссектриса, проведенная из вершины угла к основанию,является одновременно медианой и высотой, то ЕО=ОС.
∠ЕОА=∠ЕОD=90°
Так как в треугольниках ЕОD и СОD равныстороны ЕО и ОС, ОD -общая, ∠ЕОD=∠СОD=90°
эти треугольники прямоугольные и равны.
Гипотенузы ЕD и DС равны, и треугольник ЕDС - равнобедренный.
∠ ВDЕ равен разности между развернутым углом ВDС и∠ ЕDС
Из треугольника ЕDС
∠ЕDС=180-∠ОЕD-∠ОСD
∠ ОСD=∠АСD-∠АСО
Величину угла АСО найдем из равнобедренного треугольника АЕС.
∠ АЕС=∠АСЕ=(180°-116°):2=32°
∠ОСD=41°-32°=9°
∠ЕDС=180°-9°*2=162°
∠ ВDЕ=180°-162°=18°