Объяснение:
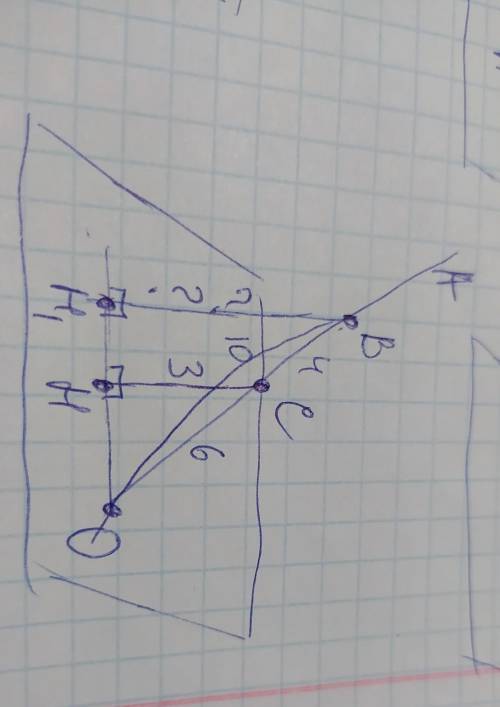
ЗАДАНИЕ 1Обозначим расстояние от точки С до плоскости СН, а расстояние до плоскости от точки В - ВН1. Рассмотрим полученные треугольники ВОН1 и СОН. Они подобны, поскольку СН и ВН1 перпендикулярны плоскости и соответственно параллельны, поэтому стороны ∆ВОН1 и ∆СОН пропорциональны. Составим пропорцию:
СО/ВО=СН/ВН1
СО×ВН1=ВО×СН
6×ВН1=10×3
6ВН1=30
ВН1=30÷6
ВН1=5
ОТВЕТ: ВН1=5ЗАДАНИЕ 2Обозначим вершины сечения КМЕ. Грань АВД пропорциональна сечению КМЕ, поскольку они параллельны. Так как части ребра ДС делятся в соотношении 2/3, то целое ребро ДС будет иметь коэффициент 2+3=5, поэтому МС/ДС=3/5. Соотношение площадей равно k²=(3/5)². Пусть площадь грани АВД=х, и зная коэффициент и площадь сечения составим пропорцию:
45/х=(3/5)²
45/х=9/25
9х=45×25
9х=1125
х=1125÷9
х=125
ответ: SАВД=125(ед²)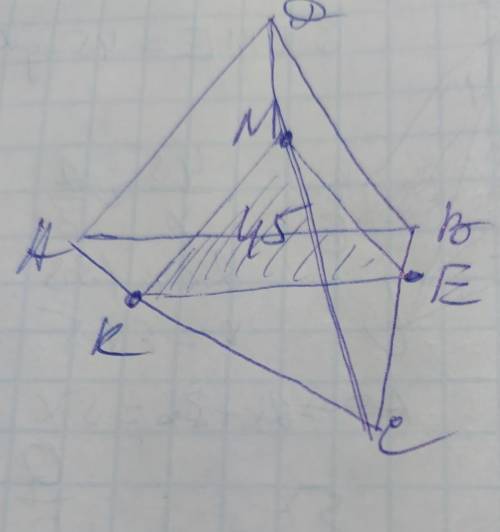
Найдем ВС. По свойству медианы, проведенной к гипотенузе, ВС=2АМ=15*2=30 см.
ВМ=СМ=30:2=15 см.
Из прямоугольного треугольника АМН найдем МН.
МН=√(АМ²-МН²)=√(225-144)=√81=9 см.
НС=МС-МН=15-9=6 см.
Из треугольника АНС найдем АС:
АС=√(АН²+СН²)=√(144+36)=√180=6√5 см.
Найдем АВ:
АВ²=ВС²-АС²=900-180=720; АВ=√720=12√5 см.
sin A=sin 90°=1
sin B=AC\BC=6√5\30=√5\5
sin C=AB\BC=12√5\30=2√5\5
ответы: 30 см; 6√5 см; 12√5 см; 1; √5\5; 2√5\5.