По условию задания треугольник АВС равнобедренный,т к АВ=ВС,а углы при основании равнобедренного треугольника равны между собой
<КАС=<С=80 градусов,тогда
<КАР=80-40=40 градусов
Треугольник АРС
Нам известны два угла,найдём третий
<АРС=180-(40+80)=60 градусов
Треугольник АКР равнобедренный
по условию задачи,т к АК=КР,тогда
<КАР=<АРК=40 градусов
<АРК=<РАС,как накрест лежащие при а || b и секущей АР
Если при пересечении прямых секущей накрест лежащие углы равны между собой,то прямые параллельны
Объяснение:
Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABC. Тогда по теореме о трех перпендикулярах OK ⊥ BC, ОМ ⊥ АС и ON ⊥ AB.
Тогда, ∠SKO = ∠SMO = ∠SNO = 45° — как линейные углы данных двугранных углов.
А следовательно, прямоугольные треугольники SKO, SMO и SNO равны по катету и острому углу.
Так что OK=OM=ON, то есть точка О является центром окружности, вписанной в ΔАВС.
Выразим площадь прямоугольника АВС:
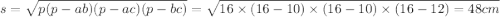
С другой стороны можно S=p×r
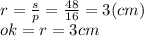
Так как в прямоугольном треугольнике SOK острый угол равен 45°, то ΔSOK является равнобедренным и SO=OK=3 см.
ответ: 3 см.
Номер 3.Нужно найти Х. Видишь диаметр, он равен 180 градусов. Значит 180-40=140