Объяснение:
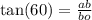
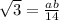
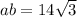
Объяснение:
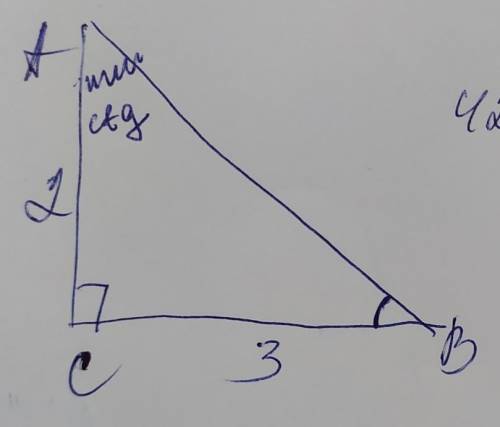
обозначим вершины треугольника А В С с прямым углом С, катетами АС и ВС и гипотенузой АВ. Найдём гипотенузу по теореме Пифагора:
АВ²=АС²+ВС²=2²+3²=4+9=13; АВ=√13
1) тангенс - это отношение противолежащего от угла катета к прилежащему катету, поэтому
tgB=AC/BC=2/3
2) углом лежащим напротив меньшего катета также будет угол В. Синус угла это отношение противолежащего от угла катета к гипотенузе поэтому sinB=AC/AB=2/√13
3) угол прилежащий к большому катету, также является <В. Косинус угла - это отношение прилежащего к углу катета к гипотенузе поэтому
cosB=BC/AB=3/√13
4) в этом случае нам нужно будет найти котангенс угла А, так как он лежит напротив большего катета ВС. Котангенс угла - это отношение прилежащего к углу катета к противолежащему:
ctg=АС/ВС=2/3
Объяснение:
По свойству касательной к окружности, радиус, проведенный в точку касания, перпендикулярен касательной, т.е. <ABO = 90°, т.е. ΔABO - прямоугольный.
Найдем AB: