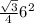=9
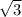. Идем дальше. Чтобы найти площадь боковой грани ADC (хотя все три равны) надо найти высоту треугольника ADC - DK. Для этого рассм. треуг. DNK. В нем угол DKN=60. Значит, KDN=180-90-60=30. Т.е. в нем DK=2NK (катет, противолежащий углу 30 гр., равен половине гипотенузы). Где возьмем NK? Из равностороннего ABC, где BK - медиана и высота, а значит ВК=
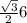=3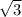. А NK=
Итак, NK=
Переходим к объему. Объем пирамиды равен одной трети произведения площади основания на высоту. В нашем случае это площадь ABC, а высота - DN. Найдем DN по теореме Пифагора из знакомого нам DNK. DN=
Уффф. Извини, что так долго ждать заставил - замучился формулы писать. Перепроверь подсчеты, а в остальном - как-то так.