Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
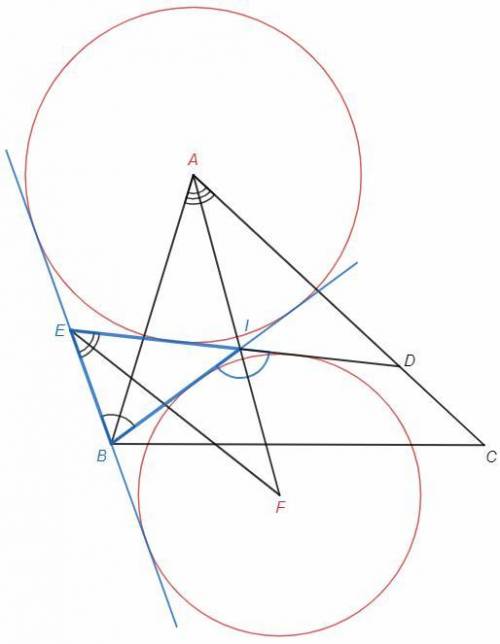
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
Объяснение:
4.
Если основание а= 3,83 см, то
Боковая сторона b=7,91 см
ответ : a=3,83 cм b=7,91 см
Если а=7,91 см, то b=3,83 cм, но такого тр-ка не существует т, к сумма двух любых сторон должна быть меньше третьей :
3,83+3,83<7,91
5.
Тр-кАВС <С=90 <А=60 СМ высота ВС=8,7 см
Найти : СМ
Решение
<В=180-<С-<А=180-90-60=30
Катет лежащий против угла 30 равен половине гипотенузе
СМ=1/2×ВС=1/2×8,7=4,35 см
6.
Тр-кАВС <С=<СВN=81
<CBM=<ABM+27
Найти <А <В
Пусть <АВМ=х
<СВМ=х+27
Сумма смежных углов равен 180
<СВМ+<СВN=180
X+27+81=180
X=180-81-27=72
<ABM=72
<CBM=72+27=99
<ABC=<CBM-<ABM=99-72=27
<A=180-<ABC-<C=180-27-81=72
ответ : <А=72 <АВС=27 <С=81