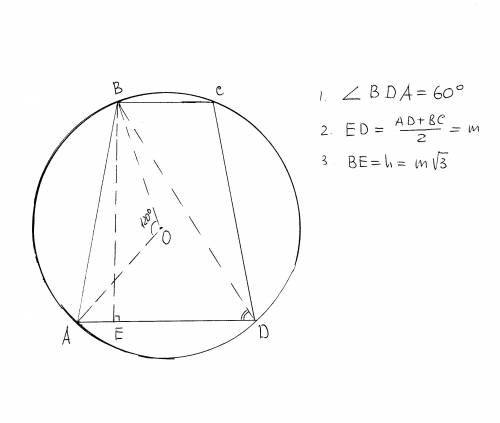
R - радиус, m - средняя линяя, h - высота трапеции, d - расстояние от центра до боковой стороны, Х - угол между боковой стороной и высотой трапеции.
Точно такой же угол Х - между средней линией и отрезком d, соединяющим центр окружности и середину боковой стороны. Углы эти равны потому что стороны их попарно перпендикулярны.
Поэтому средняя линяя равна m = 2*d*cos(X);
Легко видеть, что d = R/2, то есть m = R*cos(X)
Боковая сторона, очевидно, равна с = R*√3,
ну и высота h = с*cos(X) = R*√3*cos(X) = m*√3;
S = m^2√3 = 36√3 при m = 6
Ох я, блин :(((
В прямоугольном треугольнике, образованном высотой трапеции h, проведенной из вершины меньшего основания, диагональю трапециии и её проекцией на большее основание, угол между диагональю и большим основанием равен 60 градусам - это вписанный угол, опирающийся на ту же дугу, что и центральный угол в 120 градусов, соответствующий боковой стороне.
Поэтому проекция диагонали на большее основание равна h/√3;
Эта проекция (то есть кусочек основания между дальней вершиной и точкой-основанием высоты) равна средней линии, что показать проще простого.
(если проекция боковой стороны на большее основание а равна x, то проекция диагонали равна а - х, при этом меньшее основание b равно а - 2*х, откуда видно, что
a - x = (a + b)/2)
Отсюда сразу следует ответ :)
Решить данную задачу в 7 классе невозможно, поскольку она решается через теорему синусов, а это 9 класс! Возможно было бы решить задачу, если бы ∠BAD равнялся 115°, либо ∠BCF равнялся 55°. Тогда бы мы доказали, что ΔABC - равнобедренный и указали бы, что сторона AB равняется 5 см ( по свойству).
Что поделаешь: рассмотрим решение через теорему синусов.
Вертикальные углы равны.
⇒ ∠FCK=∠BCA=65°, так как они вертикальные.
Сумма смежных углов равна 180°.
⇒ ∠BAD+∠BAC=180°, так как они смежные ⇒ ∠BAC=180°-125°=55°.
Сумма углов треугольника равна 180°.
⇒ ∠ABC=180°-(55°+65°)=180°-120°=60°.
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
AB:sinBCA=AC:sinABC=BC:sinBAC ⇒
AB=BC*((sinBCA)/(sinBAC)) ⇒
AB=5*((sin65°)/(sin55°))≈5*(0,906/0,819)≈5,5 (см).
ответ: AB≈5,5 (см).