Найдём координаты центра окружности, используя правило нахождения среднего арифметического чисел.
Т.е. возьмём у точки "A" и точки "B" координату по оси абсцисс (Ox). Представьте, что мы должны найти среднее арифметическое чисел "6" и "-2".
Вспоминаем правило: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество (пример прикреплён ниже).
Теперь поработаем с выбранными координатами точек:
.
Теперь мы знаем, что за координата указана по оси абсцисс. Но нам ещё нужно найти координату по оси ординат (Oy).
Делаем всё по аналогии нахождения координаты оси абсцисс. Берём вторые координаты у обоих точек, которые образуют отрезок "AB". Это будут координаты "-7" и "5". Теперь находим их среднее арифметическое и получаем ответ:
Площадь прямоугольного треугольника вычисляется по формуле S=1/2*a*b, где a,b - катеты треугольника. В нашем случае S=1/2*6*8=24. Гипотенузу прямоугольного треугольника найдём по теореме Пифагора - она равна . Площадь треугольника также вычисляется по формуле S=1/2*a*h, где a - сторона треугольника, h - проведённая к ней высота. Зная площадь нашего треугольника и величину гипотенузы, найдём из этой формулы величину проведённой к гипотенузе высоты: S=1/2*a*h ⇒ h=2S/a ⇒ h=2*24/10=4.8. Таким образом, высота, проведённая к гипотенузе, равна 4.8 см.
Пусть в прямоугольный треугольник ABC вписан квадрат CDEF (см. рисунок). Здесь AC=a, BC=b. Заметим, что диагональ CE квадрата является также биссектрисой исходного треугольника. Пусть CE=d, тогда CD=d√2/2 - сторона квадрата меньше диагонали в √2 раз. Периметр квадрата равен (d√2/2)*4=2√2d, а площадь равна (d√2/2)²=d²/2. Таким образом, чтобы найти периметр и площадь квадрата, достаточно выразить биссектрису прямого угла d через a и b.
Площадь прямоугольного треугольника равна половине произведения катетов, в нашем случае S=ab/2. Теперь воспользуемся другой формулой площади - S=1/2*a*b*sin(C), где a,b - соседние стороны треугольника, а sin(C) - угол между ними. Тогда S(ACE)=1/2*AC*CE*sin(45), S(BCE)=1/2*CE*BC*sin(45) (углы ACE и BCE равны 45 градусам). Так как S(ACE)+S(BCE)=S(ABC), мы можем записать уравнение с одним неизвестным CE: 1/2*AC*CE*sin(45)+1/2*CE*BC*sin(45)=ab/2 AC*CE*sin(45)+CE*BC*sin(45)=ab CE(AC+BC)=ab/sin(45) CE=ab/(a+b)sin(45) Таким образом, d=ab/(a+b)sin(45). Получаем, что периметр квадрата равен 2√2d=2√2ab/(a+b)sin(45)=4ab/(a+b), а площадь равна d²/2=(ab/(a+b)sin(45))²*1/2=a²b²/(a+b)².
Диаметр окружности: отрезок .
.
Центр окружности: точка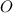 .
.
Координаты следующих точек: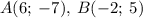 .
.
Найти нужно координаты центра окружности: .
.
Решение:Найдём координаты центра окружности, используя правило нахождения среднего арифметического чисел.
Т.е. возьмём у точки "A" и точки "B" координату по оси абсцисс (Ox). Представьте, что мы должны найти среднее арифметическое чисел "6" и "-2".
Вспоминаем правило: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество (пример прикреплён ниже).
Теперь поработаем с выбранными координатами точек:
Теперь мы знаем, что за координата указана по оси абсцисс. Но нам ещё нужно найти координату по оси ординат (Oy).
Делаем всё по аналогии нахождения координаты оси абсцисс. Берём вторые координаты у обоих точек, которые образуют отрезок "AB". Это будут координаты "-7" и "5". Теперь находим их среднее арифметическое и получаем ответ:
(чертёж к задаче прикреплён ниже)
ответ: