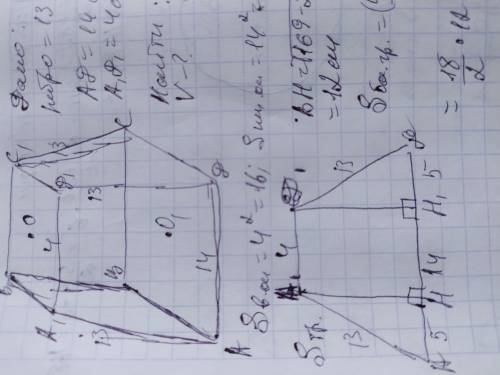
Конус;
Осевое сечение конуса - равнобедренный △АВС;
∠В = 120°;
АВ = ВС = 6 см.
Найти:V - ? (см³).
Решение:Проведём высоту ВН. Получилось два равных прямоугольных треугольника АВН и СВН (их равенство можно также доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △АВС - равнобедренный).
"Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является медианой и биссектрисой".
⇒∠АВН = ∠СВН = 120°/2 = 60°, так как ВН - биссектриса.
СН/СВ = sin ∠CBH ⇒ R = CH = CB ⋅ sin 60˚ = 6 ⋅ √3/2 = 3√3 (см).
Найдём высоту ВН, по теореме Пифагора:
с = √(a² + b²) ⇒ a = √(c² - b²), где a и b - катеты, c - гипотенуза.
a = √(6² - (3√3)²) = √9 = 3 (см).
Итак, ВН = 3 (см).
V = 1/3πR²h = π(1/3 ⋅ (3√3)² ⋅ 3) = 27π (см³).
ответ: 27π (см³).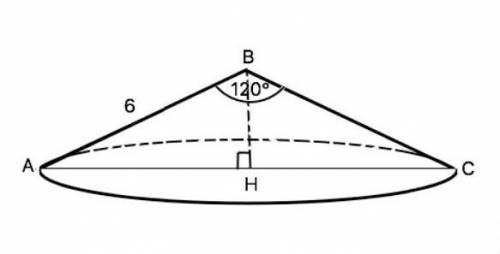
ответ: V=1072см²
Объяснение: чтобы найти полную площадь усечённой пирамиды, нужно найти площадь её боковой поверхности и площадь 2-х оснований и их суммировать. Для начала нужно найти площадь боковой грани пирамиды, ей является трапеция. Рассмотрим нашу трапецию и обозначим её вершины А А1 Д, Д1, причём А1Д1 и АД основания трапеции, а АА1 и Д1Д - боковые стороны. В нашем случае трапеция равнобедренная, поэтому АА1=Д1Д=13см.
Проведём из вершин А1 и Д1 две высоты А1Н и Д1Н1 к основанию АД. Они делят АД так что НН1=А1Д1=4см.
АН =ДН1=(14-4)/2=10/2=5см
Рассмотрим полученный ∆АА1Н. Он прямоугольный где АН и А1Н - катеты, а АА1- гипотенуза. По теореме Пифагора найдём высоту А1Н:
А1Н²=АА1²-АН²=13²-5²=169-25=144;
А1Н=√144=12см.
Теперь найдём площадь боковой грани пирамиды, зная её высоту и оба основания по формуле:
S=(A1Д1+АД)/2×А1Н=(4+14)/2×12=18/2×12=
=9×12=108см²
Sбок.гр=108см²
Так как таких граней 4, то площадь боковой поверхности будет:
Sбок.пов=Sбок.гр×4=108×4=432см²
Sбок.пов=432см²
Так как в основе правильной четырёхугольной пирамиды лежит квадрат, то площадь верхнего и нижнего основания найдём по формуле: S=a², где а- сторона квадрата.
Sверх.осн=4²=16см²
Sниж.осн=14²=196см²
Теперь найдём полную площадь поверхности усечённой пирамиды:
Sпол=Sбок.пов+S2х.осн
Sпол=432+16+196=644см²
Объём такой пирамиды вычисляется по формуле: V=⅓×h(S1+S2+√(S1×S2), где S1 и S2 площади оснований пирамиды, а h- её высота:
V=⅓×12(16+196+√(16×196))=4(212+√3136)=
=848+4√3136=848+4×56=848+224=
=1072см²
V=1072см²