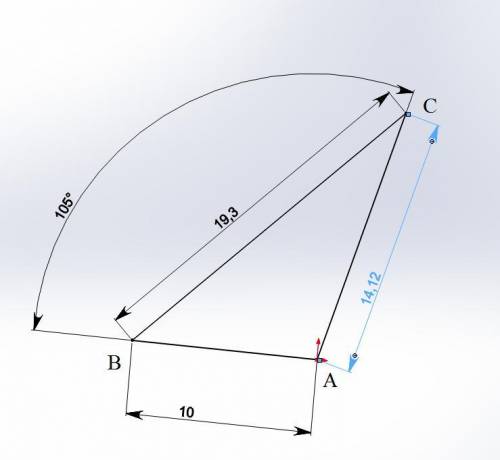
а) ∠С=30°; а=19,3 см; в=14,1 см
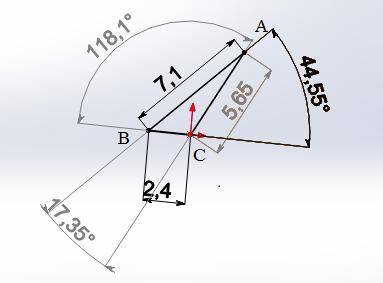
б) в=5,65 см; ∠А=17,35°; ∠С=118,1°
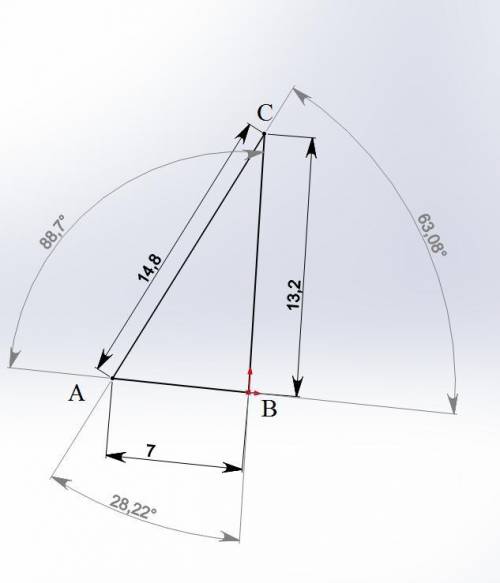
с) ∠А=63,08°; ∠В=88,7°; ∠С=28,22°
Объяснение:
а) ∠А=105°; ∠В=45°; с=10 см
∠С, а, в ?
∠С=180°-105°-45°=30°
а/sin∠А=с/sin∠С=10/sin30°=20
а=20*sin∠А=20*sin105°=19,3 см
в=20*sin∠В=20*sin45°=14,1 см
б) с=7,1 см ; а=2,4 см ; ∠В=44°33'
в, ∠А, ∠С ?
в²= а²+с²-2а*с*cos∠В=2,4²+7,1²-2*2,4*7,1*cos44°33'=31,9
в=5,65 см
sin∠А=sin∠В/в*а=sin44°33'/5,65*2,4=0,3
∠А=17,35°
sin∠С=sin∠В/в*с=sin44°33'/5,65*7,1=0,88
∠С=118,1°
с) а=13,2 см ; в=14,8 см; с=7см
а²=в²+с²-2*в*с*cos∠А
13,2²=14,8²+7²-2*14,8*7*cos∠А
cos∠А=93,8/207,2=0,45;
∠А=63,08°;
sin∠В=sin∠А/а*в=sin63,08°/13,2*14,8=0,9997
∠В=88,7°
sin∠С=sin∠А/а*с=sin63,08°/13,2*7=0,7=0,47
∠С=28,22°
Аналогично показываем, что АВ=ВС. Таким образом три стороны трапеции равны между собой.
Если за О обозначить точку пересечения диагоналей, то из рис.2 видим, что треугольники ВОС и DOA подобны (по трем углам). Причем коэффичиент подобия равен 5/13.
Обозначим за 5х - длинну основания ВС и 13х - длинну основания AD. Найдем, чему равняется KD. KD=(AD-BC)/2=(13x-5x)/2=4x.
По теореме Пифагора в прямоугольном треугольнике KCD: KD²+CK²=CD². CK - это высота трапеции, а CD=BC=5х. Тогда имеем: (4х)²+90²=(5х)² , 8100=9х², 900=х², х=30(см).
Значит ВС=5*30=150(см), а AD=13*30=390(см).
Площадь трапеции равна
S=h*(BC+AD)/2=90*(150+390)/2=90*270=24300(см²)