∠DKC = 24°.
Объяснение:
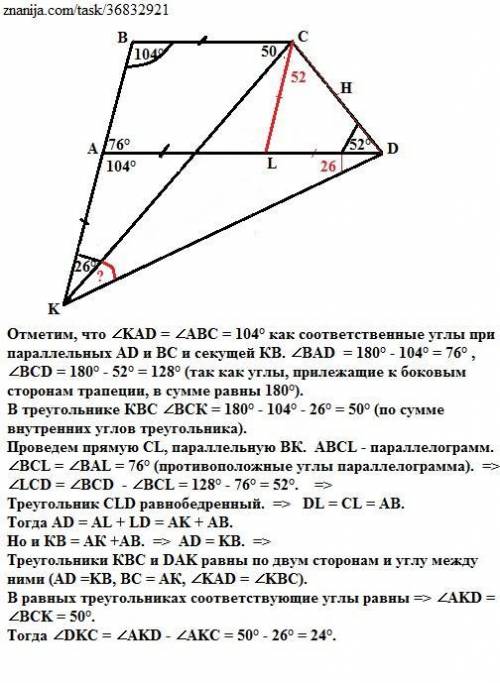
Отметим, что ∠KAD = ∠ABC = 104° как соответственные углы при параллельных AD и ВС и секущей КВ.
∠BAD = 180° - 104° = 76° , ∠BCD = 180° - 52° = 128° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).
В треугольнике КВС ∠ВСК = 180° - 104° - 26° = 50° (по сумме внутренних углов треугольника).
Проведем прямую СL, параллельную ВК.
АВСL - параллелограмм.
∠BCL = ∠BAL = 76° (противоположные углы параллелограмма). =>
∠LСD = ∠BCD - ∠BCL = 128° - 76° = 52°. =>
Треугольник СLD равнобедренный. => DL = CL = AB.
Тогда AD = AL + LD = AK + AB.
Но и КВ = АК +AВ. => AD = KB. =>
Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).
В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 50°.
Тогда ∠DKC = ∠AKD - ∠AKC = 50° - 26° = 24°.
∠DKC = 24°.
Объяснение:
Отметим, что ∠KAD = ∠ABC = 104° как соответственные углы при параллельных AD и ВС и секущей КВ.
∠BAD = 180° - 104° = 76° , ∠BCD = 180° - 52° = 128° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).
В треугольнике КВС ∠ВСК = 180° - 104° - 26° = 50° (по сумме внутренних углов треугольника).
Проведем прямую СL, параллельную ВК.
АВСL - параллелограмм.
∠BCL = ∠BAL = 76° (противоположные углы параллелограмма). =>
∠LСD = ∠BCD - ∠BCL = 128° - 76° = 52°. =>
Треугольник СLD равнобедренный. => DL = CL = AB.
Тогда AD = AL + LD = AK + AB.
Но и КВ = АК +AВ. => AD = KB. =>
Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).
В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 50°.
Тогда ∠DKC = ∠AKD - ∠AKC = 50° - 26° = 24°.

Примем сторону основания за a = 1, высоту за H = 2.
Высота h основания равна: h = a(√3/2) = √3/2.
Проекция бокового ребра на основание равна (2/3)h = (2/3)*(√3/2) = √3/3. Отсюда находим боковое ребро L:
L = √(((2/3)h)² + H²) = √((3/9) + 4) = √(13/3).
Находим апофему А:
A = √(L² - (a/2)²) = √((13/3) - (1/4)) = √(52 - 3)/12) = 7/(2√3).
Площадь боковой грани Sбг = (1/2)aA = (1/2)*1*(7/(2√3)) = 7/(4√3)).
Высота hбр из вершины основания к боковому ребру равна:
hбр = 2S/L = (2*(7/(4√3)))/√(13/3) = 7/(2√13).
Отсюда можно определить искомый двугранный угол при боковом ребре как плоский угол δ между двумя перпендикулярами к боковому ребру.
cos δ = ((hбр)² + (hбр)² - a²)/(2*(hбр)*(hбр)) = ((2*49)/(4*13) - 1)/(2*49/13) = 23/49.
δ = arccos(23/49) = 1,0822 радиан = 62,0054 градуса.