Дано :
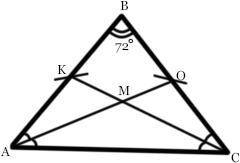
ΔАВС - равнобедренный (АВ = ВС).
∠В = 72°.
Отрезок АО - биссектриса ∠А.
Отрезок СК - биссектриса ∠С.
Точка М - точка пересечения АО и СК.
Найти :
∠АМС = ?
Углы при основании равнобедренного треугольника равны.Следовательно -
∠А = ∠С.
Сумма внутренних углов треугольника равна 180° (теорема о сумме внутренних углов треугольника).Следовательно -
∠А + ∠В + ∠С = 180°
∠А + ∠С = 180° - ∠В
∠А + ∠С = 180° - 72°
∠А + ∠С = 108°
∠А = ∠С = 108° : 2 = 54°.
Биссектриса угла треугольника - это отрезок, который является биссектрисой угла треугольника.Отсюда -
∠КАМ = ∠МАС = 54° : 2 = 27°
∠АСМ = ∠МСО = 54° : 2 = 27°.
Рассмотрим ΔАМС.
По теореме о сумме внутренних углов треугольника -
∠МАС + ∠АСМ + ∠АМС = 180°
∠АМС = 180° - ∠МАС - ∠АСМ
∠АМС = 180° - 27° - 27°
∠АМС = 126°.
126°.
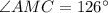
Объяснение:
Проведём биссектрисы 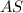 и
и 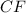 углов
углов 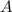 и
и 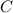 соответственно.
соответственно.
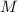 - точка пересечения биссектрис
- точка пересечения биссектрис 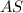 и
и 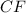 .
.
========================================================
Так как 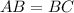

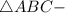 равнобедренный.
равнобедренный.

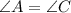 , по свойству равнобедренного треугольника.
, по свойству равнобедренного треугольника.
Сумма внутренних углов треугольника равна 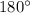 .
.
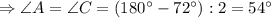
Так как 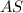 и
и 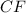 - биссектрисы углов
- биссектрисы углов 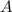 и
и 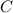 соответственно
соответственно 
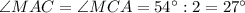
Сумма внутренних углов треугольника равна 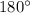
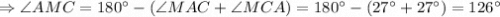
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

ответ: 126
Объяснение:
Сначала посчитаем углы A и С, а они равны, так как треугольник равнобедренный: A=C=(180-72)/2=54
Рассмотрим треугольник АМС:
Угол МАС=54/2=27(т.к. бис-са)
Угол МСА=54/2=27(т.к. бис-са)
Угол АМС=180-уголМАС-уголМСА=180-54=126