10;10
1) площадь квадрата равна площади ромба
найдём площадь ромба
пусть у нас ромб АВСД, АВ=6 см
ВД=диагональ
О центр ромба
угол АВО=60
расмотрим треугольник АВО
он прямоугольнвый
АВ гипотенуза
ВО- катет
угол АВО=60 град
ВО=AB*cos60=6*1/2=3 см
площадь треугольника будет 1/2*ВО*AO
AO=AB*sin 60=6*корень(3)/2=3*корень 3
площадь ромба будет равно площади 4 таких треугольников, то мы получим, просто 2*BO*AO=18*корень(3)
а площадь квадрата будет, сторона в квадрате
тогда получим просто, что сорона равна корень 18*корень(3)=3*2^(0.5)*3^(0.25)=3 умножить на квадратный корень с 2 и умножить на корень 4 степени с 3
2)
этот треугольник равнобедренный, так как третий угол равен 180-90-45=45
один екатет основа
другой высота
площадь равна половине произведению высоты на основу
от тут мы знаем что каеты равны
по факту половина квадрата катета
катет равен=гипотенуза* cos45=10*корень (2)/2=5*корень с 2-ух
тогда имеем, что площадь равна 1/2 *(катет)^2=1/2(5^2*2)= 1/2*50=кв. 25 см
єто и есть ответ
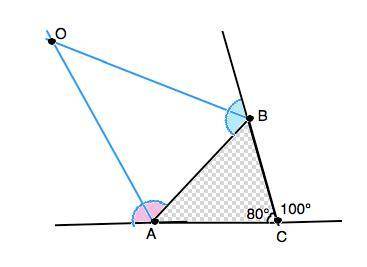
В треугольнике АВС угол С=80°. Найдите градусную меру угла АОВ, если О -точка пересечения биссектрис внешних углов треугольника при вершинах А и В.
Ответ: 50°
Объяснение: Сумма внешних углов многоугольника, взятых по одному у каждой вершины, равна 360°.
Внешний угол при С равен 180°-80°=100°. На сумму внешних углов при А и В приходится 360°-100°=260°.
Тогда в треугольнике АОВ сумма углов при вершинах А и В равна половине суммы внешних углов при А и В треугольника АВС, Т.е. ∠ОАВ+∠ОВА=260°:2=130°
Из суммы углов треугольника угол АОВ=180°-130°=50°
ОВ + ОА =R,
Радиусы перпендикулярны касательным в точках касания, поэтому
угол ОАМ = углу ОВМ = 90 гр.
Четырехугольник АМВО -квадрат, т.к все его углы прямые и две смежные стороны равны.
Диагональ этого квадрата равна ОМ = 10см, тогда сторона квадрата равна
а = √(ОМ²/2) = √50 = 5√2
ответ: АМ = МВ = 5√2
Объяснение: