АА1 = 6 см.
Объяснение:
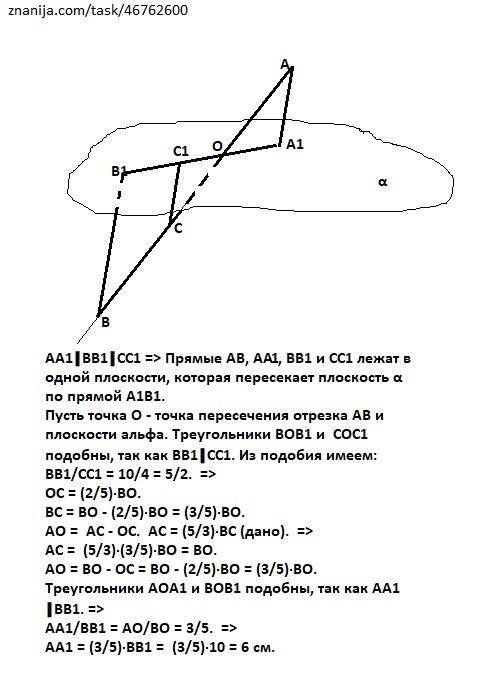
АА1║ВВ1║СС1 => Прямые АВ, АА1, ВВ1 и СС1 лежат в одной плоскости, которая пересекает плоскость α по прямой А1В1.
Пусть точка О - точка пересечения отрезка АВ и плоскости альфа. Треугольники ВОВ1 и СОС1 подобны, так как ВВ1║СС1. Из подобия имеем: ВВ1/СС1 = 10/4 = 5/2. =>
ОС = (2/5)·ВО.
ВС = ВО - (2/5)·ВО = (3/5)·ВО.
АО = АС - ОС. АС = (5/3)·ВС (дано). =>
АС = (5/3)·(3/5)·ВО = ВО.
АО = ВО - ОС = ВО - (2/5)·ВО = (3/5)·ВО.
Треугольники АОА1 и ВОВ1 подобны, так как АА1║ВВ1. =>
АА1/ВВ1 = АО/ВО = 3/5. =>
АА1 = (3/5)·ВВ1 = (3/5)·10 = 6 см.
Как получить формулу для стороны вписанного в окружность квадрата:
Можно этот квадрат разложить на четыре прямоугольных треугольника, составленных вместе- прямым углом в центре окружности. Катеты этих треугольников равны радиусу окружности, а гипотенуза (сторона квадрата) находится по теореме Пифагора:
a = √(r² + r²) = √( 2r² ) = √2 * √( r² ) = r√2
Вычислим сторону квадрата по этой формуле:
a = r√2 = (d/2)√2 = 4/2 * √2 = 2√2
Далее находим периметр квадрата- это четыре стороны:
P = 4 * a = 4 * 2√2 = 8√2 (что примерно равно 11,3)