нужна с геометрией. Площадь. От
1)Дано прямокутну трапецію, менша основа якої дорівнює 8 см. Менша бічна сторона дорівнює 4 см, а більша бічна сторона утворює з основою ∠45°.
Знайди площу трапеції.
2) Чому дорівнюють сторони прямокутника a і b , якщо вони відносяться, як 5 : 3, а площа прямокутника дорівнює 240 см2 ?
3) Висота ромба на 2 см менше, ніж його сторона. Периметр ромба дорівнює 40 см. Обчисли площу ромба.

👇

Открыть все ответы

Ответ:

SpottedJay

30.12.2020

В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
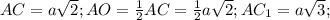
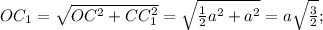
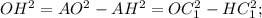
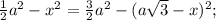
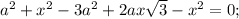
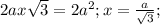
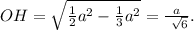
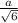
Высота, опущенная из вершины на большее основание равнобочной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
В нашем случае высота равна диаметру вписанной окружности. 2R=2S/2π =12см. Меньший отрезок большего основания у равнобочной трапеции 10/2 = 5см. Тогда по Пифагору боковая сторона равна √(12²+5²) =√169 =13см,
Средняя линия трапеции равна полусумме оснований или (в нашем случае) полусумме боковых сторон = 13см. Площадь равна средней линии, умноженной на высоту = 13см*12см = 156см²

4,5(51 оценок)

Ответ:

жанна425

30.12.2020

Кратчайшее расстояние между скрещивающимися прямыми, диагональю куба и диагональю основания куба, это расстояние между одной из двух прямых и плоскостью, проходящей через другую прямую параллельно первой прямой.
Построим плоскость, проходящую через прямую BD параллельно прямой АС1.
Возьмем точку К - середину отрезка СС1, АС1 параллельна ОК ( т к ОК средняя линия в треугольнике АСС1).
По признаку параллельности прямой и плоскости АС1 параллельна плоскости BDK. Найдем расстояние между ними, оно рано расстоянию между параллельными прямыми АС1 и ОК. Опустим перпендикуляр ОН на АС1 и найдем его длину с треугольника АОС1.
$AC=a \sqrt{2};AO= \frac{1}{2}AC= \frac{1}{2}a \sqrt{2};AC_{1}=a \sqrt{3};$
$OC _{1}= \sqrt{OC ^{2}+CC _{1} ^{2} }= \sqrt{ \frac{1}{2} a^{2}+a^{2} }=a \sqrt{ \frac{3}{2} };$

Пусть AH=x;HC1=AC1-x;

Выразим ОН из двух треугольников.
$OH ^{2}=AO ^{2}-AH^{2} =OC _{1} ^{2}-HC _{1} ^{2};$
$\frac{1}{2} a^{2}- x^{2}= \frac{3}{2} a^{2}-(a \sqrt{3}-x ) ^{2};$
$a^{2}+ x^{2}-3 a^{2}+2ax \sqrt{3}- x^{2} =0;$
$2ax \sqrt{3}=2 a^{2};x= \frac{a}{ \sqrt{3} };$

$OH= \sqrt{ \frac{1}{2} a^{2}- \frac{1}{3} a^{2} } = \frac{a}{ \ \sqrt{6} } .$

ответ $\frac{a}{ \sqrt{6} }$