1.(2б.)Знайдіть координати точок, симетричних точці А (-2; 4) відносно:
1) осі абсцис; 2) осі ординат; 3) початок координат.
2.(2б.)
Побудуйте трикутник симетричний різносторонньому трикутнику АВС
відносно точки О, яка є серединою сторони ВС.
3.(2б.).
Виконайте поворот рівнобедреного трикутника ВСК з основою ВС
на кут 900 за годинниковою стрілкою навколо точки К.
4(2б.).
Сторони трикутника дорівнюють 8 см, 7 см, 12 см. Знайдіть найменшу
сторону подібного йому трикутника, якщо його найбільша сторона дорівнює 4 см.?
5. (2б.)
.При паралельному переносі точка А(1; -3) переходить в точку В(-1;4).
В яку точку в результаті цього паралельного переносу переходить
точка С(1;-5)?
6. (2б.).
Периметри двох подібних многокутників відносяться як 2:3, а сума їх
площ дорівнює 13 см2. Знайдіть площі цих многокутників.
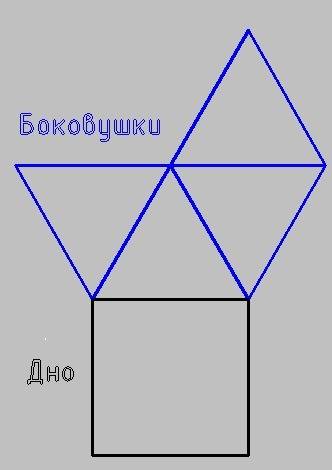
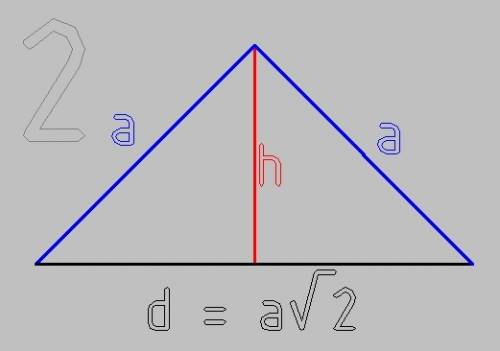
на рис.2 - диагональное сечение пирамиды, через диагональ основания и вершину
Диагональ основания по Пифагору
d² = a² + a²
d = a√2
стороны длиной а см
Видно, что это прямоугольный треугольник, точно такой же, как половинка основания
Его площадь через катеты
S = 1/2*a*a
Его площадь через гипотенузу и высоту к ней
S = 1/2*d*h
a*a = d*h
a² = a√2*h
h = a/√2 - это высота пирамиды
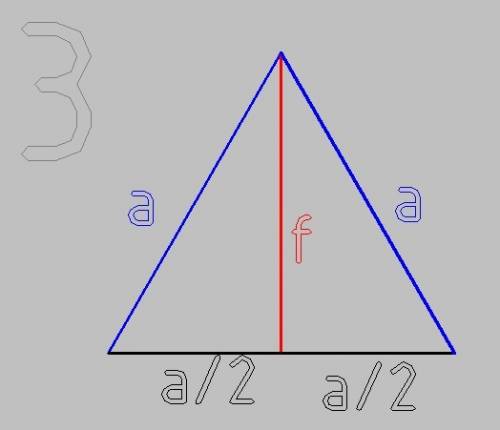
рис 3.
Боковая грань пирамиды представляет собой равносторонний треугольник - ведь все рёбра равны а
Для нахождения апофемы возьмём половину этого треугольника
По т. Пифагора
a² = (a/2)² + f²
f² = 3/4*a²
f = a√3/2
---
Площадь - это основание и 4 боковушки
S = a² + 4*1/2*a*f = a² + 2*a*a√3/2 = a²(1 + √3)
Объём
V = 1/3*a²*h = 1/3*a²*a/√2 = a³/(3√2)