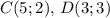или 
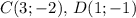
Объяснение:
Расстояние между двумя точкам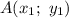и 
и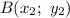 
находится по формуле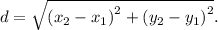 
Поэтому
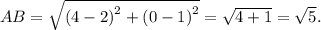
Уравнение прямой, проходящей через точки и 
имеет вид
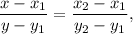
поэтому уравнение прямой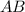 
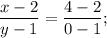
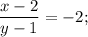
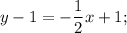
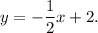
Угловой коэффициент найденной прямой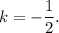 
Так как стороны квадрата перпендикулярны, уравнения прямых, которые их выражают, должны удовлетворять условию перпендикулярности с заданной прямой (для перпендикулярных прямых с угловыми коэффициентам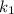и 
и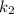 
выполняется равенство 
).
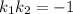Тогда угловой коэффициент прямых, проходящих перпендикулярно отрезку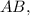 
равен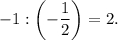 
Значит все такие прямые имеют вид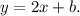 
Подставив координаты точки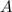 
в полученное уравнение, найдем
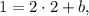
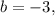
Значит уравнение прямой, перпендикулярной 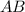и проходящей через точку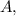 
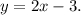
Аналогично подставив координаты точки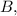 
получим
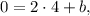
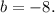
Значит уравнение прямой, перпендикулярной 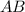и проходящей через точку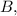 
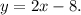
Таким образом, точка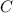 
лежит на прямой 
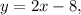т. е. ее координаты 
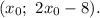А длина стороны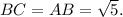 
Пользуясь формулой расстояния между двумя точками (см. выше), получаем:
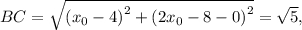
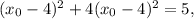
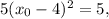
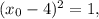
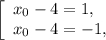
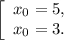
Вычисляем соответствующие значения y для этих точек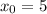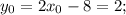: для 
для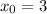 
Выходит, два возможных положения точки C —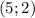 
или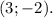 
Проделываем ту же последовательность действий для определения координат точки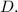 
Так как она лежит на прямой 
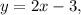то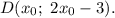 
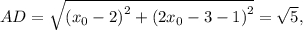
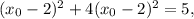
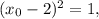
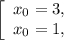
тогда 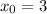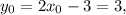для 
а для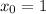 
Значит возможные положения точки 
— 
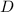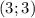или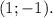 
можно было и больше поставить, задачка прикольная).. итак поехали:
стороны основания 5, 12 и 13 - это стороны прямоугольного треугольника
(25+144=169 теорема пифагора), а значит радиус вписаной окружности в основание равен р=(5+12-13)/2=2.. есть такая формула)
т.к. угол наклона у граней одинаковый, то и высоты у треугольников составляющих эти грани тоже будут одинаковы и будут составлять с высотой пирамиды и радиусом вписаной окружности в основание одинковые прямоугольные треугольники, и будут равны:
Н=корень( (4*корень(2))^2 + 2^2 ) = 6
площадь боковой поверхности пирамиды равна сумме площадей её граней, найдём каждую полупроизведением высот на их основания:
S= 5*6/2+12*6/2+13*6/2 = 15+36+39 = 90