1) Друга висота дорівнює 24 см
Объяснение:
Маємо парал. АВСД АВ=8 см , ВС=16 см , ВК(висота до сторониАД) =12 см, знайти іншу висоту до сторони СД Можна через квадратне рівняння , а можна швидче, якщо порівняти подібні трикутники АВЕ і ВКС ВЕ/АВ=ВК/ВС ВК(друга висота)=12*16/8=24 см.
2)S=48²=2304 см²
3) Р=48 знайти площу нехай Х буде стороною квадрата , 4Х=48 , Х=12 S=12²=144 см²
4) позначимо сторону прямокутника через Х, друга буде 5Х , складемо периметр:2х+10х=44 12х=44 х=3,7 , друга сторона =5*3,7=18,5 S=18,5*3,7=68.5 см²
5) S =1/2*27*22=297 см²
6)S= 1/2*13*14=91см²
Формула площади боковой поверхности конуса
S=π r l
где r-радиус его основания, - l- образующая.
Радиус и образующую предстоит найти.
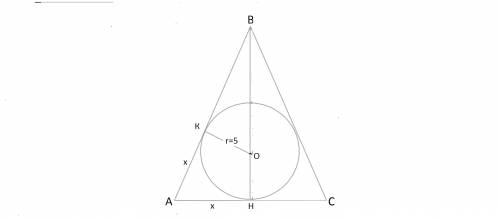
Сделаем рисунок осевого сечения конуса и шара, вписанного в него.
Это сечение - равнобедренный треугольник с вписанной в него окружностью.
Рассмотрим прямоугольный треугольник ВКО.
ВО = высота без радиуса
ВО=18-5=13
Тогда ВК, как сторона треугольника с отношением Пифагоровой тройки равна 12
( можно проверить т. Пифагора, получится такая же длина ВК)
В треугольнике АВН отрезок АК=АН как части касательных к окружности.
Пусть они равны х.
Тогда АВ=12+х.
АВ²=ВН²+АН²
(12+х)²=18²+х²
144+24х+х²=324+х²
24х=180
х=7,5
Радиус основания конуса равен 7,5
Образующая равна 12+7,5=19,5
S=π r l=π*7,5*19,5=146,25π или ≈ 459,458
Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 6 см и 12 см и периметром 36 см
Объяснение:
АВСМ- описанная трапеция⇒ суммы длин противоположных сторон равны. Т.е 6+12=АВ+СМ⇒ АВ=СМ=9 см. Пусть ВК⊥АМ , СР⊥АМ.
S(круга)=πr². Радиус вписанной в трапецию окружности будет равен половине высоты трапеции.
Т.к. ВК⊥АМ , СР⊥АМ, то КВСР-прямоугольник ⇒КР=6 см, АК=РМ=(12-6) :2=3 (см).
ΔАВК-прямоугольный, по т. Пифагора ВК=√(9²-3²)=√18=3√2(см). ВК-высота трапеции, значит r=(3√2)/2 см.
S(круга)= π ( (3√2)/2 )²=4,5π (см²)