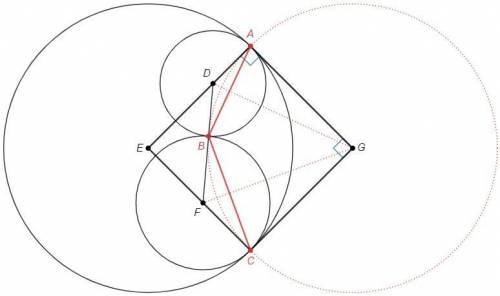
Центр G описанной окружности △ABC лежит на пересечении серединных перпендикуляров к сторонам AB и BC. Серединный перпендикуляр к хорде является биссектрисой центрального угла. DG - биссектриса ADB, FG - биссектриса BFC. Точка G является пересечением биссектрис внешних углов △DEF и центром вневписанной окружности.
EA=EC, DA=DB, FC=FB (радиусы)
ED+DA=EF+FC => ED+DB=EF+FB
Точка B делит периметр △DEF пополам, следовательно является точкой касания вневписанной окружности.
GB - радиус вневписанной окружности △DEF, следовательно GA также радиус этой окружности, A - точка касания. Радиус в точку касания перпендикулярен касательной, A=90.
EAGC - ромб (стороны равны как радиусы равных окружностей) с прямым углом A, следовательно квадрат, G=90.
∪AC=90, ∪CA=360-90=270, ABC=270/2=135
В данном случае нам понадобится узнать синус угла А,так как этот угол будет противолежащим стороне бц,а если мы его узнаем,то и узнаем сам радиус.
Для этого находим угол а,угол А=180 градусов-(угол С+ угол Б)=180-(64+56)=60.
Мы знаем ,то синус 60 градусов равен корень из 3 / 2,тогда радиус окружности равен отношению БЦ/2*синус угла А,следовательно 3 корней из 3/ 2* корень из 3/2.При умножении в знаменателе двойки сокращаются,следовательно 3 корней из 3/корень из 3=3.Так как при делении корни дают 1.