Сейчас идет дистанционка заданий много времени нет сделайте с развернутыми ответами
Вариант №1
Часть А
1 Если сумма двух углов равна 180°, то эти углы:
а)вертикальные б) определить невозможно в) смежные
2 Один из углов, полученных при пересечении двух прямых, больше другого на 40°.
Найдите меньший угол.
3 Какое наименьшее число лучей может выходить из одной точки, чтобы все углы,
образованные соседними лучами, были не острыми?
4 Периметр равнобедренного треугольника равен 19 см. Одна из его сторон равна 3
см. Найдите длины двух других сторон.
5 Один из соответственных углов, образованных при пересечении прямых n и m,
секущей k, больше другого. Определите взаимное расположение прямых n и m.
а) пересекаются б) параллельны в) такая ситуация невозможна.
6 Определите вид треугольника, если разность двух его углов равна третьему углу.
а) остроугольный в)тупоугольный
б)прямоугольный г) определить невозможно
7 Углы треугольника относятся как 5:2:5. Определите вид данного треугольника.
по углам: по сторонам:
1.остроугольный 1.разностороний
2.прямоугольный 2.равносторонний
3.тупоугольный 3.равнобедренный
8 Сколько различных треугольников можно составить из пяти отрезков, длины
которых равны 1см,2см,4см,5см,6см?
Часть В
1 В треугольнике АВС высота ВD является биссектрисой треугольника. Найдите
периметр треугольника АВС, если периметр треугольника АВD равен 17 см, а
высота ВD равна 6 см.
2 ВМ – медиана треугольника АВС. Прямая АD перпендикулярна медиане и делит ее
пополам. Сравните длины АВ и АС.
3 Треугольник АСВ прямоугольный, СD высота. Найдите гипотенузу АВ, если
ВС=6см, ВD=3см.
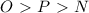- всё это конечно углы.
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
теперь подставим наши значения в эту пропорцию:
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см