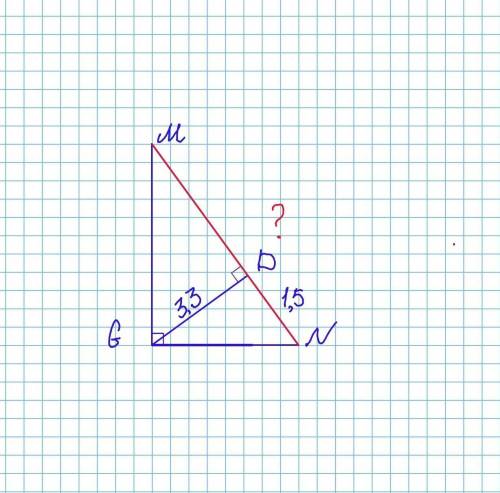
В прямоугольном треугольнике MNG высота GD, проведенная из прямого угла, равна 3,3. Найди значение гипотенузы MN, если один из её отрезков, на которые делит высота GD, равен 1,5.
Объяснение:
Дано: ΔMNG(∠G = 90°), GD - высота, GD⊥ MN, GD = 3,3 ед, DN = 1,5 ед
Найти: гипотенузу MN-?
Теорема: Высота, которую провели из вершины прямого угла на гипотенузу, численно равна среднему геометрическому проекций обоих катетов на эту гипотенузу.
Данную теорему можно записать так:
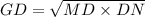
MD - проекция катета MG на гипотенузу MN, DN - проекция катета GN на гипотенузу MN.
DN = 1,5 ед, GD = 3,3 ед.
Найдём MD:
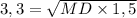
3,3² = MD•1,5
10,89=MD•1,5
MD=10,89 ÷ 1,5 = 7,26 ед
Тогда гипотенуза MN = MD + DN = 7,26 +1,5 = 8,76 ед.
Два круга имеют внутреннее прикосновение в точке А, причем меньше круг проходит через центр большей. Докажите, что любая хорда большей круги, которая выходит из точки А, делится меньшим кругом пополам.
Дано:окр С(R=CA) ,окр В (r=ВА) ,СА=2ВА, внутреннее касание в точке А.
Доказать :что любая хорда большего круга, выходящая из точки А, делится меньшей окружностью пополам.
Доказательство.
Пусть АМ-хорда большей окружности , пересекает меньшую окружность в точке Р. Необходимо доказать , что Р-середина АМ или АМ=2АР.
1)ΔАМС- равнобедренный , т.к СА=СМ=R, значит ∠1=∠3.
2) ΔАРВ-равнобедренный , т.к ВА=ВР=r, значит ∠2=∠3.
ΔАМС подобен ΔАРВ по двум углам : ∠1= ∠2 , ∠3-общий . В подобных треугольниках сходственные стороны пропорциональны :
СА:ВА=АМ:АР или 2ВА:ВА=АМ:АР или 2:1=АМ:АР , АМ=2АР , значит Р-середина.
Объяснение: