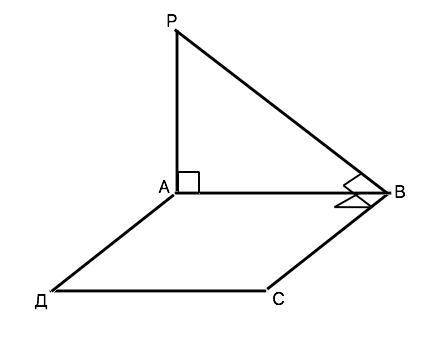
РА - перпендикуляр к площади параллелограмма АВСД. Укажите вид параллелограмма, если РВ перпендикулярен ВС. а) ромб, б) прямоугольник; в) квадрат.
Объяснение: РВ - наклонная. АВ - её проекция на плоскость АВСД. По т. о 3-х перпендикулярах если наклонная (РВ) перпендикулярна прямой (ВС) на плоскости, то её проекция на ту же плоскость перпендикулярна данной прямой. Следовательно, АВ⊥ВС, и угол АВС - прямой. Противоположные углы параллелограмма равны. ⇒ ∠Д=∠В=90°, поэтому из суммы углов четырехугольника ∠А+∠С=360°-2•90°=180°, и каждый из них равен 180°:2=90°.
Углы четырехугольника АВСД прямые. ⇒ АВСД - прямоугольник. Он может быть и квадратом. если его стороны будут равны.
Площадь боковой поверхности треугольной призмы состоит из суммы площадей трех ее граней, которые являются прямоугольниками. Площадь одной грани будет равна 72/3=-24 см. В призме высота равна ребру, т.е. одной из сторон прямоугольной грани и равна 6 см. по условию задачи. Найдем длину стороны основания, которая является и стороной грани призмы из формулы площади прямоугольника ах6=24, т.е. сторона а = 4. Т.к. в основании правильной треугольной призмы лежит равнобедренный треугольник (все его стороны и углы равны), то можем вычислить его площадь
S= 1/2х4х4хsin60=8√3/2=4√3