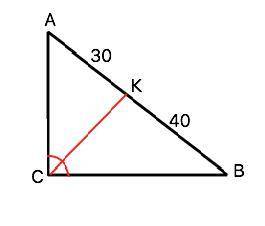
Бисектриса прямого угла прямоугольного треугольника делит гіпотенузу на отрезки 40 см и 30 см. Найдите периметр треугольника.
Обозначим треугольник АВС; СК - биссектриса. АК=30 см, ВК=40 см.
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. (свойство). АК:ВК=30:40=3:4. =>
АС:ВС=3:4. Из отношения катетов видно, что треугольник АВС - так называемый «египетский» с отношением сторон 3:4:5. .
Примем коэффициент отношения равным а.
Тогда АС=3а, ВС=4а, гипотенуза АВ=5а.
АВ=АВ+ВК=30+40=70 (см) => а=70:5=14(см).
Р=3а+4а+5а=12а
Р=12•14=168 (см)
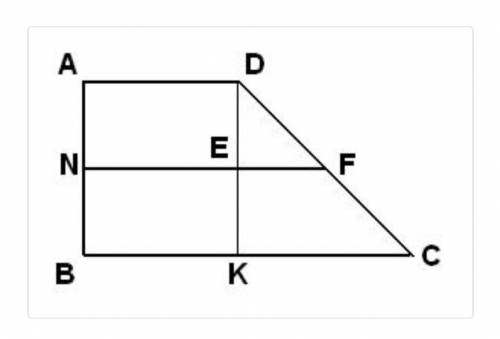
Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Объяснение:
DK – перпендикуляр к ВС (см.рисунок). Так как NF - средняя линия трапеции, то AN = NB = DE = EK = AB/2 = 12/2 = 6 cм. Поскольку угол BCD = 45 градусов, то и угол NFD = 45. Тогда DE = EF = 6 см. Следовательно NE = BK = AD = NF – EF = 20 – 6 = 14 cм. В треугольнике DKC EF – его средняя линия. Посему KC = 2EF = 2*6 = 12 см. Таким образом ВС = ВК + КС. Но выше было найдено, что ВК = NE = AD = 14 см. Тогда ВС = 14 + 12 = 26 см. ВС можно было бы найти и иначе. Помните? Средняя линия трапеции равна полусумме оснований. Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Рассмотрим синий треугольник со сторонами 13,14, 15
Его полупериметр
p = (13+14+15)/2 = 21 см
Площадь по формуле Герона
S₁² = 21*(21-13)*(21-14)*(21-15)
S₁² = 21*8*7*6 = 21*16*21
S₁ = 21*4 = 84 см²
Площадь через высоту к стороне 14
S₁ = 1/2*14*h = 84 см²
h = 12 см Высота красной трапеции и высота синего треугольника совпадают Площадь трапеции S = 1/2(a+b)*h = 1/2(10+4)*12 = 84 см²