1) ∠SAD = 30°.
2) ∠ASO = 30°.
3) ∠SAC = 60°.
4) ∠SHO = 30°.
Объяснение:
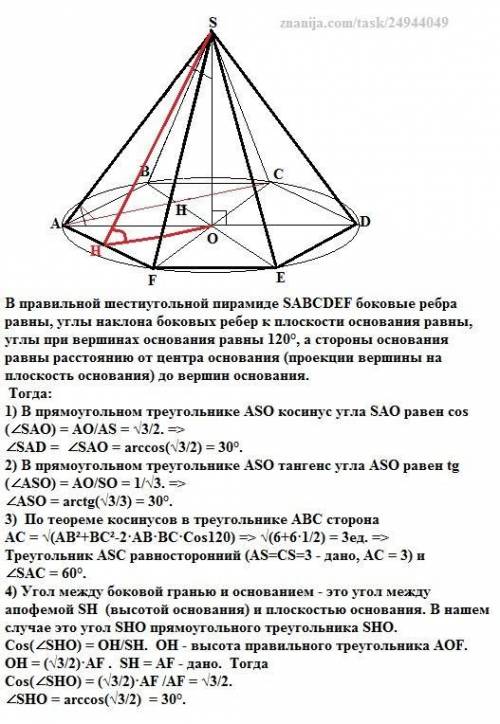
В правильной шестиугольной пирамиде SABCDEF боковые ребра равны, углы наклона боковых ребер к плоскости основания равны, углы при вершинах основания равны 120°, а стороны основания равны расстоянию от центра основания (проекции вершины на плоскость основания) до вершин основания.
Тогда:
1) В прямоугольном треугольнике АSО косинус угла SAO равен сos(∠SAO) = АО/AS = √3/2. =>
∠SAD = ∠SAO = arccos(√3/2) = 30°.
2) В прямоугольном треугольнике АSО тангенс угла АSO равен tg(∠ASO) = АО/SO = 1/√3. =>
∠ASO = arctg(√3/3) = 30°.
3) По теореме косинусов в треугольнике АВС сторона
АС = √(АВ²+ВС²-2·АВ·ВС·Cos120) => √(6+6·1/2) = 3ед. =>
Треугольник АSС равносторонний (AS=CS=3 - дано, АС = 3) и
∠SAC = 60°.
4) Угол между боковой гранью и основанием - это угол между апофемой SH (высотой основания) и плоскостью основания. В нашем случае это угол SHO прямоугольного треугольника SHO.
Cos(∠SHO) = OH/SH. OH - высота правильного треугольника AOF.
OH = (√3/2)·AF . SH = AF - дано. Тогда
Cos(∠SHO) = (√3/2)·AF /AF = √3/2.
∠SHO = arccos(√3/2) = 30°.
Так как заданий много, пишу кратко. Извиняйте, Вам жалко пунктов, а мне времени.
1) Пусть меньшая сторона - х см, тогда вторая - (х+13) см.
х+х+13=47
2х=34
х=17
ответ. 17 см.
2) Данный прямоугольник является квадратом - все стороны равны.
d=a√2
a = d/√2 = 16√2 / √2 = 16.
Р=4а=4·16=64
ответ. 64.
3) 7х+5х=180
12х=180
х=15
7·15=105°, 5·15=75°
105°-75°=30°
ответ. 30°.
4) углы, которые соединяет диагональ, равны по 23°+38°=61°
два других угла равны по 180°-61°=119°
ответ. 119°
5) 154° - это сумма противоположных углов. Так как они равны, то каждый из них равен 154°:2=77°.
Два других равны по 180°-77°=103°
ответ. 103°
6) Третий угол равен 180°-123°=57°, четвертый угол - 180°-71°109°.
Меньший из всех - 57°.
ответ. 57°.
Проводим высоту к основанию, она делит его на 2 равных отрезка по 6 см. Находим высоту по теореме пифагора √10²-6²=√64=8
S(площадь)=8×10×0.5=40 см²