30
Объяснение:
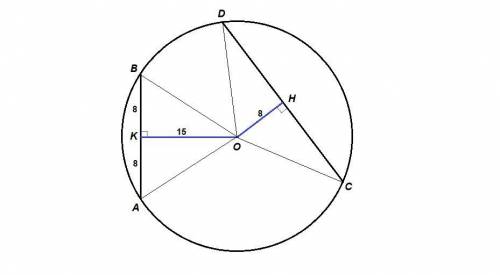
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30
я сделала рисунок, чтобы было понятнее (см. вложение)
пирамида SABC, ее высота SO=2, высота боковой грани SH, биссектриса, медиана и она же высота основания AH, угол SHO=30 градусов(это линейный угол двугранного угла SBCA)
искомая площадь-площадь боковой поверхности, т.е. три площади одной боковой грани:
S=3*0,5*a*h , где a-сторона основания, a=CB,
h-высоты бок. грани, h=SH
найдем SH из треуг. OSH:
катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, т.е.
SH=2*SO=2*2=4 ,т.е. h=4
найдем СB из треуг. ACB:
СB=2*корень(3)*r=2*корень(3)*OH=2*корень(3)*корень(16-4)=2*корень(3)*корень(12)=2*корень(3)*2*корень(3)=4*3=12 ,т.е. a=12
подставляем все значения в первую формулу и получаем:
S=3*0,5*12*4=6*12=72 см^2