1.В прямоугольном треугольнике ABC (угол В- прямой) угол C:угол A=1:3. Определите, чему равны углы треугольника. - id1225534620200731 от gfg9y 31.07.2020 03:53

Question

Геометрия: 1.В прямоугольном треугольнике ABC (угол В- прямой) угол C:угол A=1:3. Определите, чему равны углы треугольника. 2.Дано: угол AOD = 90°, угол 0AD = 60°, угол 0CB = 30°. Доказать: AD || BC. 3.В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DЕ.​

gfg9y · Accepted Answer

Можно и с рисунком.
Касательные к окружности, проведённые из одной точки, равны.
Обозначим равные отрезки как показано на рисунке через x, y и z.
AB=x+z, AC=x+y.
По теореме биссектрис АС/АВ=СД/ВД,
(x+y)/(x+z)=y/z,
xz+yz=xy+yz,
xz=xy,
z=y.
СД/ВД=у/z=1, значит АС/АВ=1, значит АВ=АС.
Треугольник АВС - равнобедренный, в нём АД - высота и биссектриса, центр вписанной окружности лежит на биссектрисе, вписанная окружность касается стороны ВС в точке Д, но это не значит, что АВ=ВС. Это равенство может быть только если тр-ник АВС правильный, но это лишь частный случай.
Не доказано.
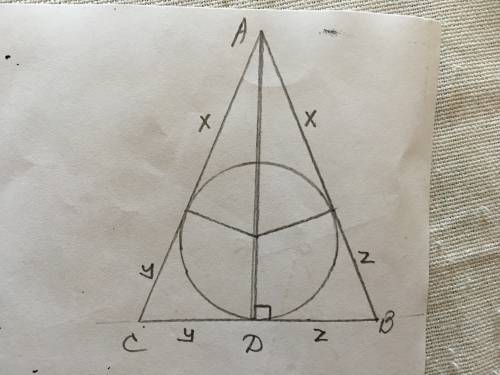
Окружность вписанная в треугольник авс касается стороны вс в точке d. докажите что если луч аd - бис

Окружность вписанная в треугольник авс касается стороны вс в точке d. докажите что если луч аd - бис

MOGZ ответил