Объяснение:
1. Начертим четырехугольник MKPE. Проведем отрезки, соединяющие две несоседние вершины - диагонали MP и KE.
2. Не знаю.
3. Начертим четырехугольник BCKM. KC и BM - это соседние стороны KM.
4. Так как в четырехугольнике BCOE все 4 угла равны по 90°, то это - прямоугольник. А так как параллельны только стороны BC и OE, то это не параллелограмм.
5. Нет. Так как в параллелограмме точка пересечения диагоналей делит эти диагонали пополам.
6. Параллелограмм.
7. Тут мы просто 2,5 и 3,5 умножим на 2. Получим 5 и 7 см. Задачка некорректная, так как диагонали в параллелограмме должны быть равны.
8. Периметр параллелограмма находится по формуле P = 2(AB + BC)
Составим уравнение:
2(3 + BC) = 20
раскроем скобки:
6 + 2BC = 20
2BC = 14
BC = 7
9. Угол A - острый, следовательно, он будет равен 45 градусам.
По признаку параллелограмма углы, лежащие друг напротив друга - равны. А также сумма углов, прилежащих к одной стороне, равна 180 градусов.
Сразу отметим, что угол C = 45 градусов, так как он лежит против угла А.
Угол B равен 180 - 45 = 135 градусов. Угол D равен 135 градусов, так как он лежит напротив угла B.
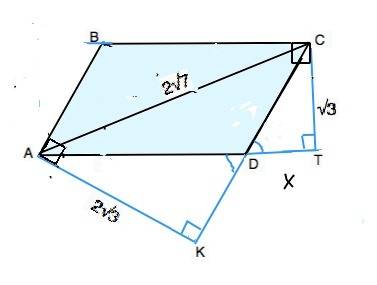
Обозначим параллелограмм АВСD. Проведем высоты из вершин острых углов параллелограмма. Они пересекутся с продолжениями сторон. СТ- высота к АD , АК - высота к СD. Прямоугольные треугольники АКD и СТD подобны по равному острому углу при D ( они вертикальные). k=AK:CT=2. Отношение площадей подобных фигур равно квадрату их коэффициента подобия. ⇒ S(AKD)=4S(CTD)
Из ∆ АСТ по т.Пифагора АТ=5. Из ∆ АСК по т.Пифагора СК=4. Площадь половины параллелограмма S(АСD)=S(ACT)-S(CTD). Она же равна S(ACK)-S(AKD) Подставим в уравнения известные значения и приравняем их. 0,5•5•√3 - S(CTD)=0,5•4•2√3 -4S(СТD), откуда получим S(CTD)=(3√3):6=0,5√3
Ѕ АВСD=2•S(ACD)=2•[(0,5•5•√3-0,5√3)]=4√3 ⇒ S²=(4√3)²=48
В треугольнике АВС, АВ=6 корней из 2 см, АС=6 корней из 3 см, угол В=60 градусов. Тогда больший угол треугольника АВС будет равен___
Объяснение:
По т. синусов "Стороны треугольника пропорциональны синусам противолежащих углов " получаем
АС/sinВ=АВ/sinС, (6√3)/sin60°=(6√2)/sinС , sinС=√2/2, ∠С=45°
sinС=1/√2, sinС=√2/2, ∠С=45°
По теореме о сумме углов треугольника ∠А=180-60°-45°=75°.
Больший угол ΔАВС будет ∠А=75°