ΔАВС: АВ=ВС, <В=50° Биссектриса АК угла А при основании делит угол А на 2 равных <ВАК=<САК. Медиана ВМ, проведенная к основанию, делит основание на АМ=МС; также она является и высотой и биссектрисой (<АВМ=<СВМ=50/2=25°). Медиана ВМ и биссектриса АК пересекаются в точке О Нужно найти угол АОВ. В равнобедренном треугольнике углы при основании равны, значит <А=<С=(180-<В)/2=(180-50)/2=65°. Тогда <ВАК=65/2=32,5° Из ΔАВО найдем <АОВ=180-<АВО-<ВАО=180-25-32,5=122,5°=122°30'
ΔАВС: АВ=ВС, <В=50° Биссектриса АК угла А при основании делит угол А на 2 равных <ВАК=<САК. Медиана ВМ, проведенная к основанию, делит основание на АМ=МС; также она является и высотой и биссектрисой (<АВМ=<СВМ=50/2=25°). Медиана ВМ и биссектриса АК пересекаются в точке О Нужно найти угол АОВ. В равнобедренном треугольнике углы при основании равны, значит <А=<С=(180-<В)/2=(180-50)/2=65°. Тогда <ВАК=65/2=32,5° Из ΔАВО найдем <АОВ=180-<АВО-<ВАО=180-25-32,5=122,5°=122°30'
Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=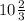 3 см ⇒
3 см ⇒
Диаметр АС=АМ+МС=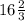 см⇒
см⇒