ответ: 10 см.
Объяснение:
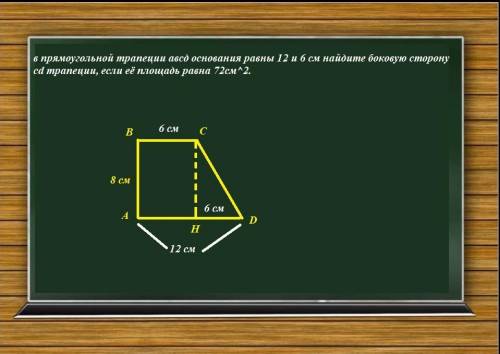
в прямоугольной трапеции авсд основания равны 12 и 6 см найдите боковую сторону сd трапеции, если её площадь равна 72см^2.
Решение
S=h(a+b)/2, где S=72 см^2 площадь трапеции; а=12 см - нижнее основание, b=6 см - верхнее основание: h - высота в см.
h(12+6)/2=72;
18h/2=72;
9h=72;
h=72:9;
h=8 см - высота трапеции.
Проведем высоту СН трапеции.
(См. скриншот).
В полученном треугольнике CDH CH=8 см; DH=12-6=6 см. Тогда по т. Пифагора
CD²=СH²+DH²=8²+6²=64+36=100;
CD=√100=10 см.
Объяснение:
считаем что точки являются концами диаметра
координаты центра окружности будут серединой отрезка АВ
по формуле координат середины отрезка
x₀=(x₁+x₂)/2
y₀=(y₁+y₂)/2
x₀=(-3+0)/2=-1,5
y₀=(2-2)/2=0
по формуле расстояния между двумя точками
AB=√((x₁-x₂)²+(y₁-y₂)²)=√((-3-0)²+(2+2)²)=√(9+16)=√25=5
R=AB/2=5/2=2.5
уравнение окружности с центром в точке (x₀;y₀) и радиуса R
(x-x₀)²+(y-y₀)²=R²
В нашем случае x₀=-1,5; y₀=0 ; R=2.5
уравнение окружности
(x+1.5)²+y²=2.5² или
(x+1.5)²+y²=6.25
проверка
(-3+1.5)²+2²=1.5²+2²=2.25+4=6.25
(0+1.5)²+(-2)²=1.5²+2²=2.25+4=6.25
1)BDD1
2)DD1A
3)A1B1C1