Объяснение:
Выполним построение треугольника ABC.
Так как треугольник ABC тупоугольный, то его высота будет опущена на продолжение треугольника ABC.
Когда мы провели высоту AD, то у нас образовалось два прямоугольных треугольника: DBC и DCK.
Так как треугольники прямоугольные, то в них будет действовать теорема Пифагора. Но нам неизвестно DC. Мы можем найти весь катет BD:
BD^2 = AB^2 - AD^2 = 17^2 - 8^2 = 225
BD = 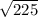 = 15
= 15
Можем найти DC: 15 - BC = 15 - 9 = 6 см
А теперь AC находим по теореме Пифагора:
AC^2 = AD^2 + DC^2 = 8^2 + 6^2 = 64 + 36 = 100
AC = 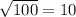

Дано:AB=8
Угол А=30
Найти BC,AC,Sabc
Решение:
1) По свойству прямоугольного треугольника катет лежащий против угла в 30 градусов равен половине гипотенузы => BC = 8:2=4см
2)По теореме пифагора найдём AC
AC^2=AB^2-BC^2=√8^2-4^2= √64-16 = √64 - √16 = 8-4=4см
3) По формуле 1/2ah найдём площадь треугольника - 1/2 4*4= 16:2=8см^2
ответ: BC=4,AC=4,S=8см^2
Задача №2.
Дано: NK=4
Угол M=45 градусов
Найти MK,MN
Решение:
1) Сперва для решения задачи найдём угол N по сумме углов треугольника,угол N = 180-(90+45)=180-135=45 градусов
2) Так как угол M = углу N = 45 градусов,то треугольник равнобедренный,значит NK=KM=4см
3) По теореме Пифагора найдём гипотенузу
NM^2=NK^2+KM^2= √4^2+4^2 = √16+16
= √16 + √16 = 4+4 =8см
ответ: MK=4см,NM = 8см