Question

Дано:вд=да=дс,угл с=40° найти :угл а, угл авс

Answer 1

Объяснение:

ΔBDC - равнобедренный т.к. BD = DC ⇒

1) ∠BCD = ∠DCB = 40 ⇒ ∠ BDC = 180 - 40 x 2 = 100

2)  ∠BDA = 180 - 100 = 80

BDA -  равнобедренный т.к. BD = AD ⇒

3) ∠ABD = ∠DAB = (180 - 80) : 2 = 50

4)  50 + 40 = 90 (∠ABC)

ответ:  ∠ABC = 90, ∠A = 50

Answer 2

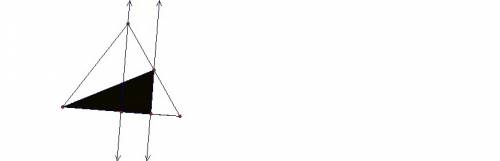
Дано:

BD = DA = DC

∠C = 40˚

Найти:

∠A; ∠ABC.

Решение.

Т.к. BD = DA = DC => △ABD и △DBC - равнобедренные

∠DBC = 40˚ (угол при основании)

∠BDC = 40 + 40 = 180 - 80 = 100˚

∠BDA = 180 - 100 = 80˚

∠A = ∠ABD , т.к. △ABD - равнобедренный.

∠A = ∠ABD = (180 - 80) : 2 = 50˚

=> ∠ABC = 40 + 50 = 90˚

ответ: 50˚; 90˚.