Чему равен вписанный угол,который упирается на дугу, градусная мера которой равна 44°?

👇

Увидеть ответ

Ответ:

Aleks19102007

10.09.2022

ответ: 22°

Объяснение:

Вписаный угол равен половине дуги на которую он опирается. Следовательно вписанный угол равен половине 44° то есть 22°

4,4(36 оценок)

Открыть все ответы

Ответ:

kustsireni

10.09.2022

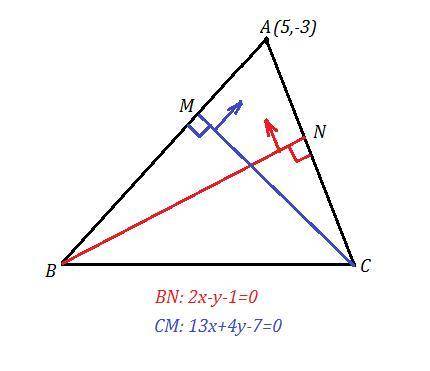
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

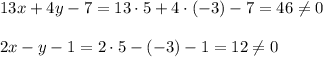
$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

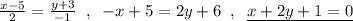
$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

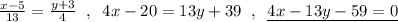
$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

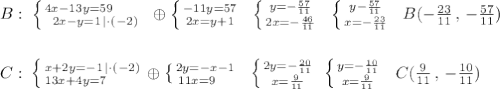
$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$

Даны уравнения прямых, содержащих высоты треугольника, и координаты одной из вершин треугольника. вы

4,4(92 оценок)

Ответ:

nyanchann

10.09.2022

Углы при основании у равнобедренной трапеции равны, значит второй угол тоже 60°.

Так как при диагонали угол 30°, то 60-30=30°

Сумма всех углов 360°

360°-60°-60°=240°

240°:2=120° (остальные два угла

рассмотрим верхний треугольник с меньшим основанием. 180°-120°-30°=30°, следовательно два угла одинаковые. Это равнобедренный треугольник.

Если боковая сторона 4 см, то и меньшее основание тоже 4 см.

Рассмотрим треугольник, который образует диагональ, с нижним основанием трапеции. 180°-60°-30°=90°. Значит он прямоугольный, в котором боковая сторона 4 см - катет, лежащий против угла 30° и равен половине гипотенузы.

Большее основание трапеции является гипотенузой этого треугольника.

Большее основание равно 4*2=8 см

ответ: основания трапеции 4 см и 8 см.

4,5(92 оценок)

Это интересно:

Транспорт

28.04.2020

Как заменить ручки на руле мотоцикла: подробное руководство...

Стиль-и-уход-за-собой

12.09.2021

Хочешь меньше волос? Простые способы решения проблемы!...

Компьютеры-и-электроника